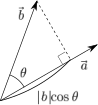
- ベクトルの内積（2次元） ベクトル\(\vec{a}\),\(\vec{b}\)の内積は以下のように定義される。
- 証明 ベクトル\(\vec{a}\),\(\vec{b}\),\(\vec{c}\)で構成される以下のような三角形を考える。
- 内積の性質
内積には\(\cdot\)（ドット記号）を用いる。 \[ \vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta \] \(\vec{a}\),\(\vec{b}\)の要素を以下のようにすると \[ \vec{a}=(a_x,a_y)\\ \vec{b}=(b_x,b_y) \] 内積は以下のように書くことができる。 \[ \vec{a}\cdot\vec{b}=a_xb_x+a_yb_y \]
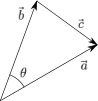余弦定理より
\[
|\vec{c}|^2=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos\theta
\]
\(\vec{c}=\vec{a}-\vec{b}\)より
\[
\begin{eqnarray}
(a_x-b_x)^2+(a_y-b_y)^2&=&(a_x^2+a_y^2)+(b_x^2+b_y^2)-2|\vec{a}||\vec{b}|\cos\theta\\
a_x^2+a_y^2+b_x^2+b_y^2-2a_xb_x-2a_yb_y&=&a_x^2+a_y^2+b_x^2+b_y^2-2|\vec{a}||\vec{b}|\cos\theta\\
|\vec{a}||\vec{b}|\cos\theta&=&a_xb_x+a_yb_y
\end{eqnarray}
\]
| 鋭角のとき(0°<θ<90°) | 直角のとき(θ=90°) | 鈍角のとき(90°<θ<180°) | 向きが同じで平行のとき(θ=0°) | 向きが反対で平行のとき(θ=180°) |
| \[\vec{a}\cdot\vec{b}>0\] | \[\vec{a}\cdot\vec{b}=0\] | \[\vec{a}\cdot\vec{b}<0\] | \[\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\] | \[\vec{a}\cdot\vec{b}=-|\vec{a}||\vec{b}|\] |
- 外積
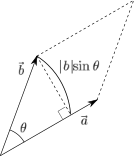
- ベクトルの外積（2次元） ベクトル\(\vec{a}\),\(\vec{b}\)の外積は以下のように定義される。
- 証明 \[ \begin{eqnarray} |\vec{a}||\vec{b}|\sin\theta&=&|\vec{a}||\vec{b}|\sqrt{1-\cos^2\theta}\\ &=&|\vec{a}||\vec{b}|\sqrt{1-\frac{(\vec{a}\cdot\vec{b})^2}{(|\vec{a}||\vec{b}|)^2}}~~~~(\because\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta)\\ &=&\sqrt{(|\vec{a}||\vec{b}|)^2-(\vec{a}\cdot\vec{b})^2}\\ &=&\sqrt{(a_x^2+a_y^2)(b_x^2+b_y^2)-(a_xb_x+a_yb_y)^2}\\ &=&\sqrt{a_x^2b_y^2-2a_xa_yb_xb_y+a_y^2b_x^2}\\ &=&\sqrt{(a_xb_y-a_yb_x)^2}\\ &=&a_xb_y-a_yb_x \end{eqnarray} \]
- 外積の性質
- \(\vec{a}\times\vec{b}\neq \vec{b}\times\vec{a} \)
- \(\vec{a}\times\vec{b}= -(\vec{b}\times\vec{a}) \)
- 二つのベクトルを２辺とする平行四辺形の面積に相当する
- 1/2倍すれば二つのベクトルを２辺とする三角形の面積になる
-
\[\vec{a}\times\vec{b}>0\] \[\vec{a}\times\vec{b}=0\] \[\vec{a}\times\vec{b}<0\] \(\vec{b}\)は\(\vec{a}\)の右側 \(\vec{b}\)は\(\vec{a}\)と平行 \(\vec{b}\)は\(\vec{a}\)の左側
外積には\(\times\)（クロス記号）を用いる。 \[ \vec{a}\times\vec{b}=|\vec{a}||\vec{b}|\sin\theta \] \(\vec{a}\),\(\vec{b}\)の要素を以下のようにすると \[ \vec{a}=(a_x,a_y)\\ \vec{b}=(b_x,b_y) \] 外積は以下のように書くことができる。 \[ \vec{a}\times\vec{b}=a_xb_y-a_yb_x \]
- Christer Ericson（著）中村達也（訳）ゲームプログラミングのためのリアルタイム衝突判定
- Eric Lengyel（著）狩野 智英（訳）ゲームプログラミングのための3Dグラフィックス数学
- https://math.keicode.com/vector-calculus/gaiseki-menseki.php
- http://izumi-math.jp/G_Kakuta/in_pro/in_pro.htm