- 直線と点の衝突判定 直線は長さが無限大のまっすぐな線で、コンピュータ上での表現の仕方としては様々な方法があるが、 今回は直線上の点(大抵の場合始点)とベクトル(始点とは異なる直線上の点)で表すものとする。
- 線分と点の衝突判定 線分は始点と終点が明示的に定義された有限の長さをもつまっすぐな線である。
直線と任意の点が交差しているか調べる方法の一つとして外積を用いた方法があげられる
直線ベクトル\(\vec{a}\)と直線の始点と点を結ぶベクトル\(\vec{b}\)の外積をとり、 \[ \vec{a}\times\vec{b}=0 \] となれば、同じ始点のベクトルでかつ平行になるので点は直線上にある、すなわち交差していると言える。 このようにして直線と点の交差判定を行う

線分と点との交差判定を行うには、理論上無限の長さを持つ直線とは異なり点が線上にあり、始点と終点の間に存在する必要がある。
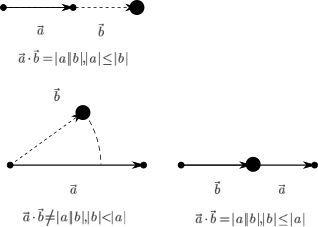
線分と点の交差判定を行う方法の一つとして、内積を用いた方法があげられる。 内積の性質より、線分の始点と終点を結ぶベクトル\(\vec{a}\)と線分の始点と点を結ぶベクトル\(\vec{b}\)に以下の関係 \[ \vec{a}\cdot\vec{b}=|a||b| \] あるいは \[ \vec{a}\cdot\vec{b}-|a||b|=0 \] が成り立てば、少なくとも線分の視点から終点の延長線上に点が存在することが言える。 さらにベクトル\(\vec{b}\)の長さ\(|b|\)がベクトル\(\vec{a}\)の長さ\(|a|\)より短ければ点は線分上にあり交差していると言える。