Javaプログラミング

立体形状の表示

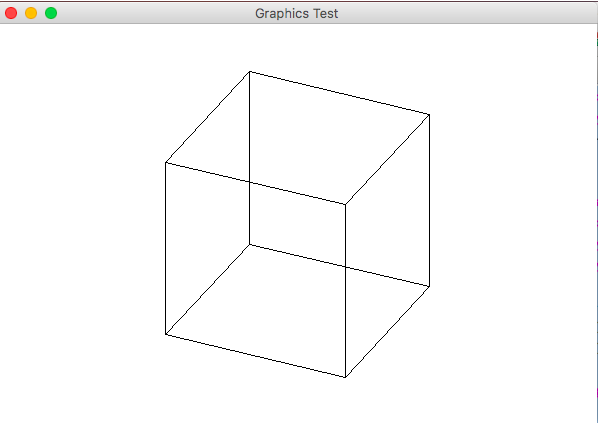
• 3次元から2次元への変換
立体形状は幅、高さ、奥行きをもつ3次元図形である。
これをコンピュータディスプレイ等の画面や紙などの2次元平面上に表示する為には、
3次元から2次元への変換が必要である。この変換を投影という。
2次元座標系に3次元座標系を投影する場合、幅、高さに加えて仮想的な奥行きを考える必要がある。
コンピュータのスクリーンの水平方向を幅、鉛直方向を高さとした場合、
視点からスクリーンに向かう方向あるいはスクリーンから視点に向かう方向を奥行きと考えることができる。

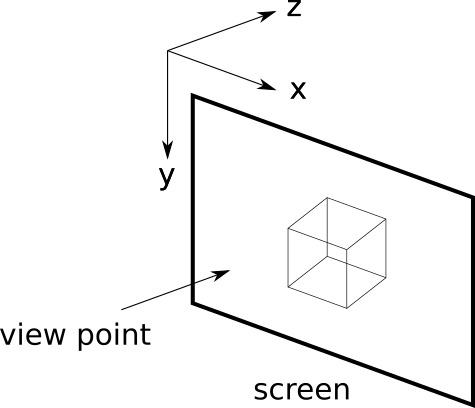
3次元図形の投影と座標系
スクリーンの左から右に向かう方向を正（+x）、スクリーンの上から下に向かう方向を(+y)とした場合、
視点からスクリーンへ向かう方向を正(+z)とする場合、その座標系は右手系(Right-hended coordinate system), 逆にスクリーンから視点へ向かう方向を正(+z)とする場合、その座標系は左手系(Left-hended coordinate system)という. 以降特に断りがない場合を除き、右手系の座標系として考える。
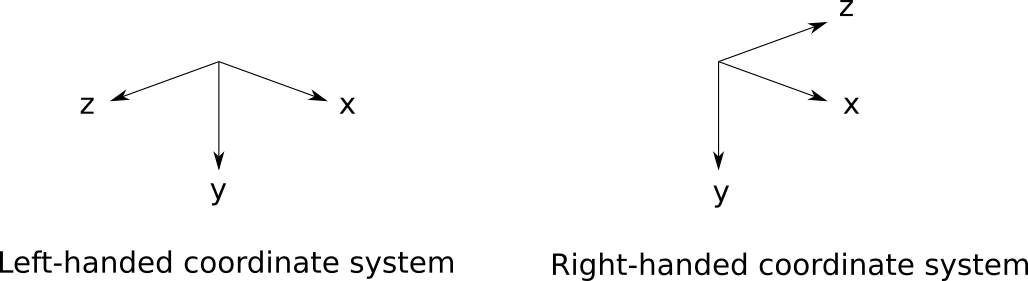
左手系と右手系
• 立方体の表示と回転変換
以下のような中心を原点(x,y,z)=(0,0,0)に持つ１辺の長さが200の立方体の表示を行う。
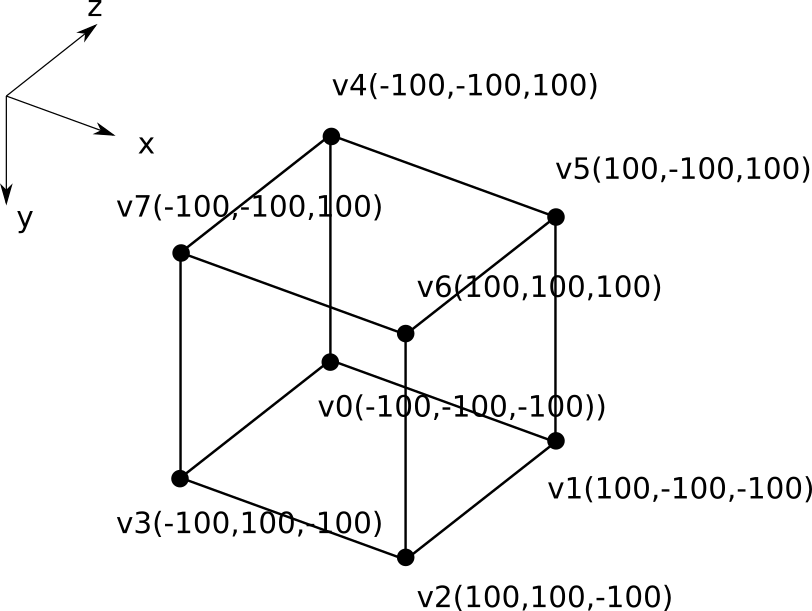
立方体
これをそのままx-y平面上に投影するとスクリーン上には以下のように表示される。
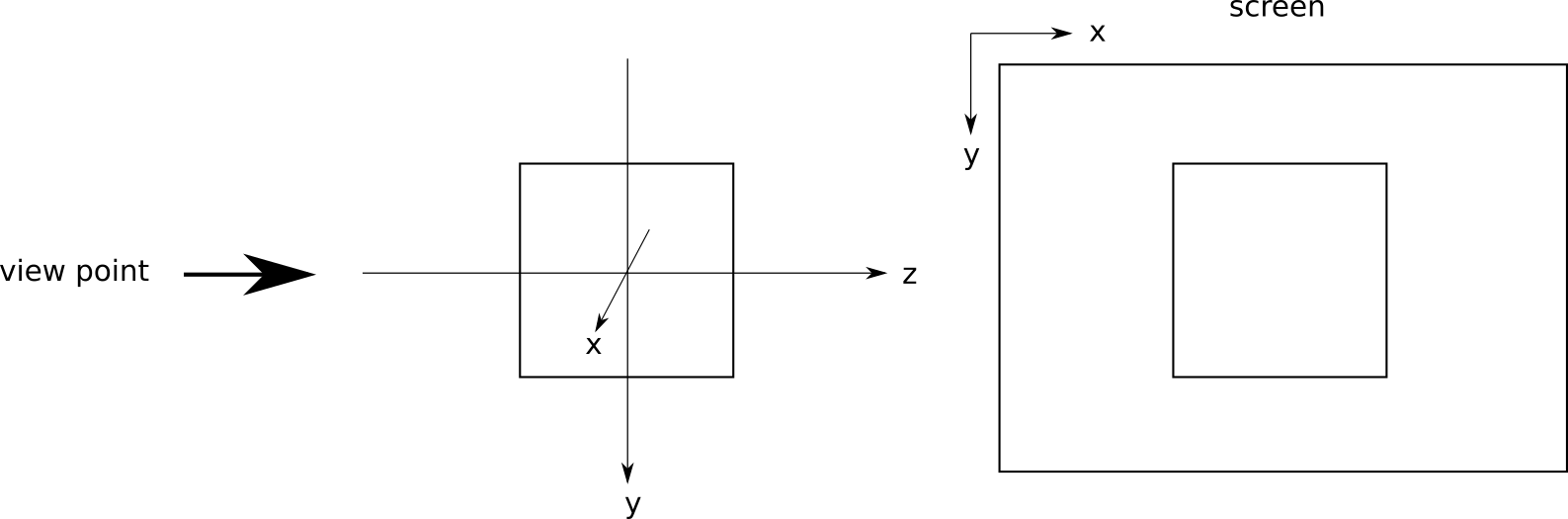
立方体のx-y平面への投影
この投影ではx軸方向とy軸方向の2軸分の2次元の情報しか表示されていない。
この状態からx軸,y軸,z軸の3軸分の独立した情報を表示するには最低２軸以上の回転変換が必要になる。
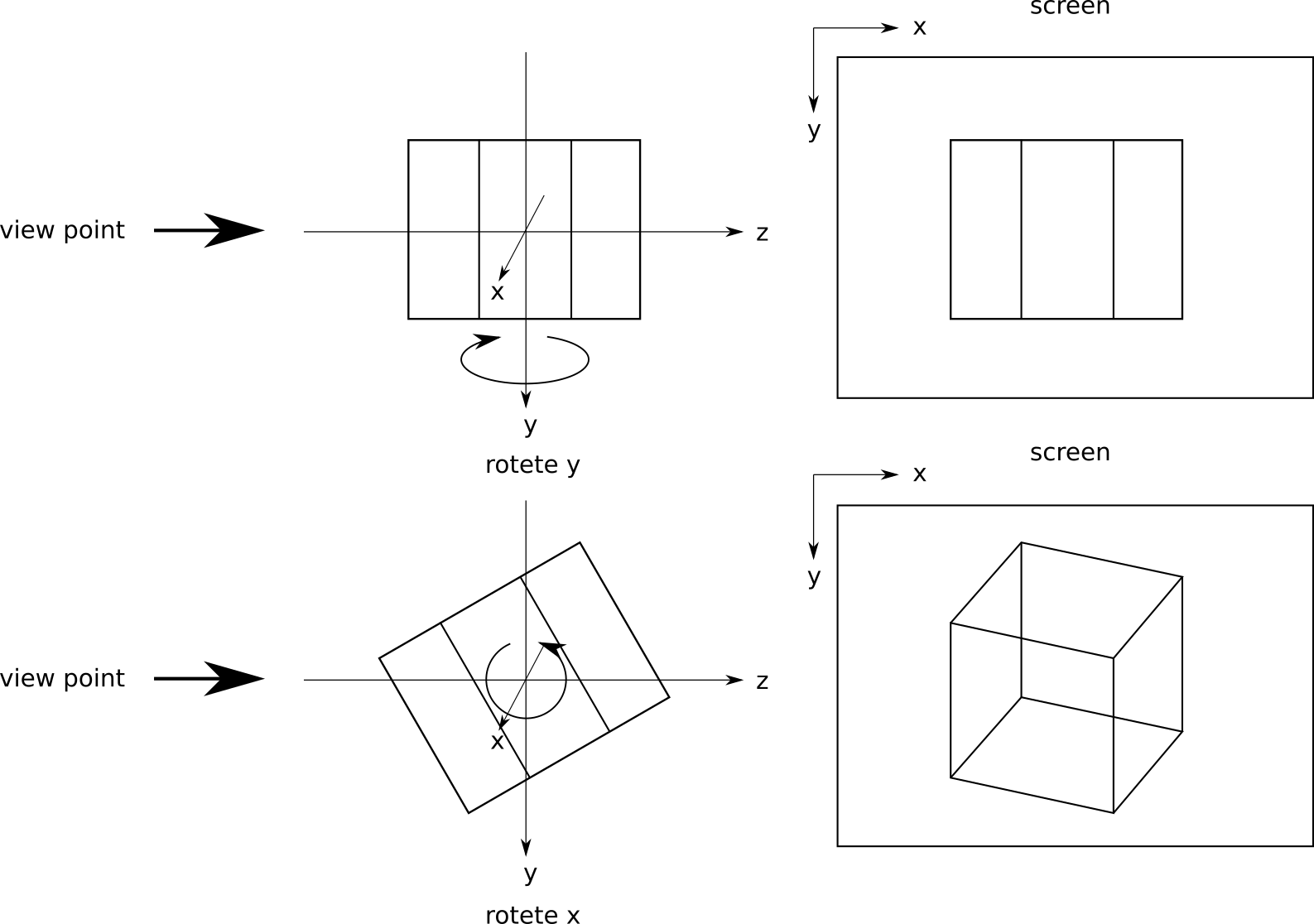
y軸、x軸の2軸の回転変換
• 回転変換
右手系の座標系の場合、x軸、y軸、z軸はそれぞれ右ねじの法則に従って回転する。
すなわち各軸を正の方向から見た場合、反時計回りを正方向として回転する。
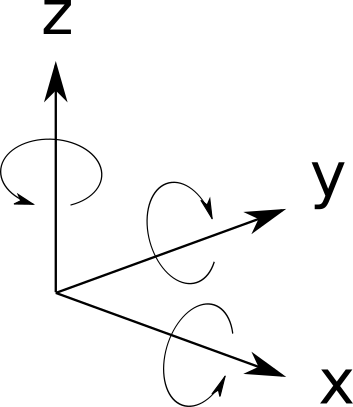
右手系の各軸の回転方向
その結果、x軸の回転はy軸をz軸に向ける方向、y軸の回転はz軸をx軸に向ける方向、z軸の回転はx軸をy軸に向ける方向になる
各軸の回転後の座標
• x軸の回転変換
\[ v\prime_x=v_x\\ v\prime_y=\cos(\alpha+\beta)\\ v\prime_z=\sin(\alpha+\beta) \] 加法定理より \[ v\prime_y=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\ v\prime_z=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\ \] \(v_x=\cos\beta\)、\(v_y=\sin\beta\)より、 \[ v\prime_x=v_x\\ v\prime_y=v_y\cos\alpha-v_z\sin\alpha\\ v\prime_z=v_y\sin\alpha+v_z\cos\alpha \]
• y軸の回転変換
\[ v\prime_x=\cos(\beta-\alpha)\\ v\prime_y=v_y\\ v\prime_z=\sin(\beta-\alpha) \] 加法定理より \[ v\prime_y=\cos\beta\cos\alpha+\sin\beta\sin\alpha\\ v\prime_z=\sin\beta\cos\alpha-\cos\beta\sin\alpha\\ \] \(v_x=\cos\beta\)、\(v_z=\sin\beta\)より、 \[ v\prime_x=v_x\cos\alpha+v_z\sin\alpha\\ v\prime_y=v_y\\ v\prime_z=-v_x\sin\alpha+v_z\cos\alpha \]
• z軸の回転変換
\[ v\prime_x=\cos(\alpha+\beta)\\ v\prime_y=\sin(\alpha+\beta)\\ v\prime_z=v_z \] 加法定理より \[ v\prime_x=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\ v\prime_y=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\ \] \(v_x=\cos\beta\)、\(v_y=\sin\beta\)より、 \[ v\prime_x=v_x\cos\alpha-v_y\sin\alpha\\ v\prime_y=v_x\sin\alpha+v_y\cos\alpha\\ v\prime_z=v_z \]
• 原点座標の移動
これまでは３次元空間状で原点を中心にもつ立方体について考えてきたが、スクリーンは左上を原点とする座標系であるため スクリーンの座標系を画面中央に変換する必要がある。
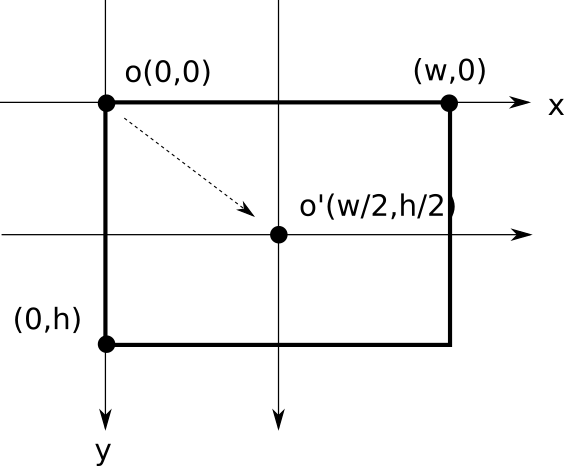
原点座標の移動
今回は画面の左上の原点oを画面中央の原点o'に変換する為に 投影画像の座標の水平成分にスクリーンの幅の1/2、鉛直成分に高さの1/2をそれぞれ平行移動することで座標変換を行う。 すなわち \[ v_x\prime=v_x+width/2\\ v_y\prime=v_y+height/2\\ \] あるいは \[ v_x\prime=v_x+o\prime_x\\ v_y\prime=v_y+o\prime_y\\ \]
• プログラムによる実装
画面の右方向を+x,画面の下方向を+yとした右手系座標において25°の角度でy軸回転、30°の角度でx軸回転した立方体を画面中央に表示するプログラムを以下に示す。
コード

		import java.awt.Canvas;
		import java.awt.Color;
		import java.awt.Graphics;
		
		import javax.swing.JFrame;
		
		public class DrawCube extends Canvas{
			public int screenW=600;
			public int screenH=400;
		
			public DrawCube() {
				setSize(screenW,screenH);
				setBackground(Color.white);
				setForeground(Color.black);
		
				JFrame f=new JFrame();
		
				f.setTitle("Graphics Test");
				f.setSize(screenW,screenH);
				f.setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
				f.add(this);
				f.pack();
				f.setVisible(true);
			}
		
			public void paint(Graphics g) {
				//立方体の頂点の定義
				double[][] vertices= {
						{-100,-100,-100},
						{ 100,-100,-100},
						{ 100, 100,-100},
						{-100, 100,-100},
						{-100,-100, 100},
						{ 100,-100, 100},
						{ 100, 100, 100},
						{-100, 100, 100}
				};
		
				//立方体の面の定義
				int[][] faces= {
						{0,1,2,3},
						{1,5,6,2},
						{2,6,7,3},
						{3,7,4,0},
						{0,4,5,1},
						{6,7,4,5},
				};
		
		
				int[] px=new int[4];
				int[] py=new int[4];
				for(int i=0;i<6;i++) {
					for(int j=0;j<4;j++) {
						double x=vertices[faces[i][j]][0];
						double y=vertices[faces[i][j]][1];
						double z=vertices[faces[i][j]][2];
		
						//y軸回転
						double alpha=25*Math.PI/180;
						double x1=x*Math.cos(alpha)+z*Math.sin(alpha);
						double y1=y;
						double z1=-x*Math.sin(alpha)+z*Math.cos(alpha);
		
						//x軸回転
						double beta=30*Math.PI/180;
						double x2=x1;
						double y2=y1*Math.cos(beta)-z1*Math.sin(beta);
						double z2=y1*Math.sin(beta)+z1*Math.cos(beta);
		
						//座標原点移動
						px[j]=(int)x2+screenW/2;
						py[j]=(int)y2+screenH/2;
					}
					g.drawPolygon(px, py, 4);
				}
		
			}
		
			public static void main(String[] args) {
				new DrawCube();
			}
		}


実行結果

---

←前へ      次へ→