- 投影図 投影図は3次元立体物を2次元平面上に写したものである。
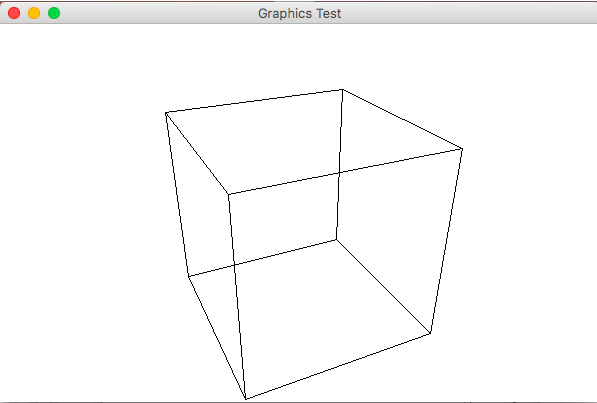
- 透視投影 透視投影(もしくは、中心投影)は視点から離れるほど像が小さくなり、最終的には1点に集束するような投影方法で、目やカメラで映る像と同様の図が得られる。
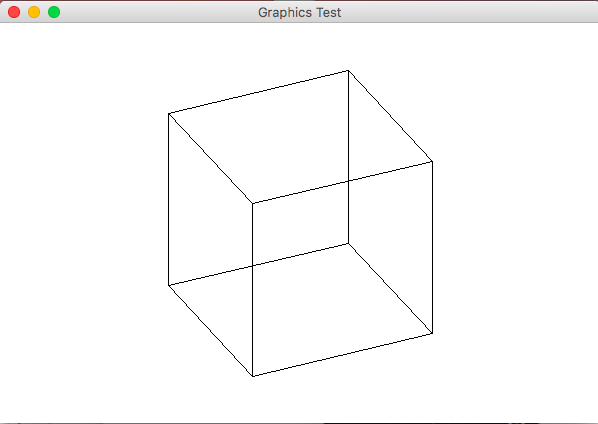
- 平行投影 平行投影は視点から遠く離れても像の大きさが同じになるような投影方法で、3次元図形の任意の天から投射線を平行に投影面に投射し、 その平面上に投影図を作る。
- プログラムによる実装 画面の右方向を+x,画面の下方向を+yとした右手系座標において25°の角度でy軸回転、30°の角度でx軸回転した立方体を それぞれ透視投影したもの、平行投影したものを表示するプログラムを以下に示す。 コード(透視投影)
3次元空間内に視点(投影中心)を置き、投影対象の3次元形状の任意の点と視点を結ぶ直線を 投影面と呼ばれる2次元平面に写し、それらを結ぶことで得られる。
投影図には投影の方法により大きく分けて透視投影と平行投影がある。
コンピュータスクリーンに3次元形状を表示する場合、この投影図を利用する。
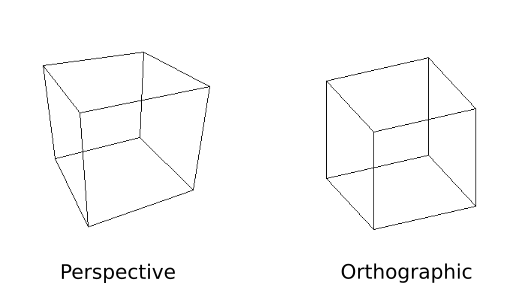
透視投影(Perspective projection)と平行投影(Orthogonal projection)
面を正面に向けた透明な立方体を少し離れた視点から投影すると以下のようになる。
立方体の透視投影
視点に近い手前の面は大きく投影され、逆に視点から離れた奥の面は手前の面に比べて小さく投影されている。ここで3次元形状を透視投影した時に得られる座標について考える。
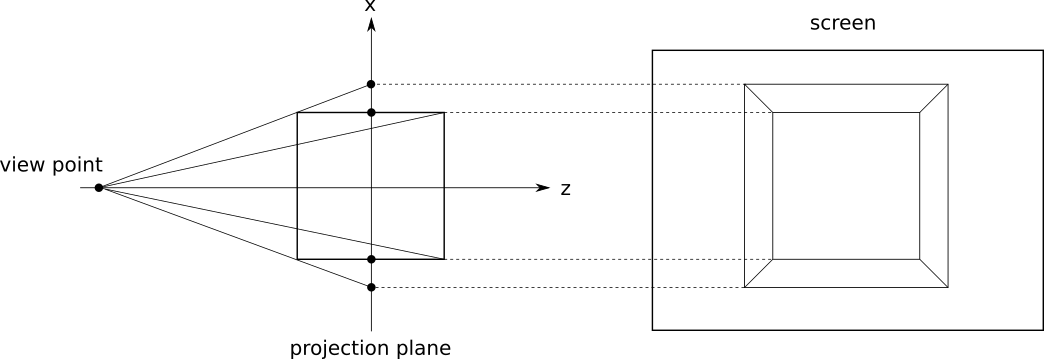
以下のようなz-x平面上において原点を中心に持つ立方体があったとして、これをz軸上の視点\(z_0\)から見て\(z=0\)の平面(視点に垂直でz-x平面と直交するx軸を通る平面)を投影面とする。
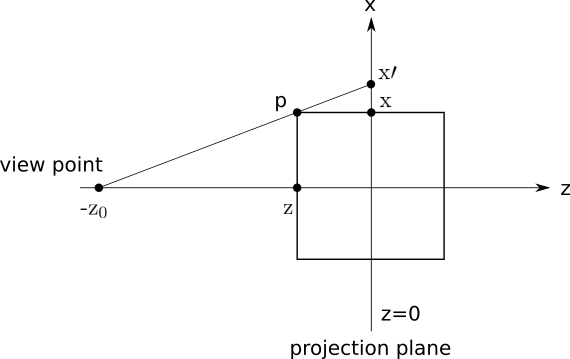
透視投影による座標の変換
このとき、立方体上の点pに着目して投影による変換後の座標を\(x\prime\)としてこれを求める。
視点\(z_0\)と立方体上の点pを結ぶ直線を
\[
x=az+b
\]
とすると傾き\(a\)は
\[
a=\frac{x}{z_0-z}
\]
となり、視点\((z,x)=(z_0,0)\)を通るので、\(b\)は
\[
b=\frac{x}{z_0-z}z_0
\]
投影後の座標\(x\prime\)は
\[
x\prime=\frac{x}{z_0-z}z_0
\]
となる
これを変形して以下のように書くことができる
\[
x\prime=\frac{x}{1-\frac{z}{z_0}}
\]
同様に考えてy軸については以下のようになる
\[
y\prime=\frac{y}{1-\frac{z}{z_0}}
\]
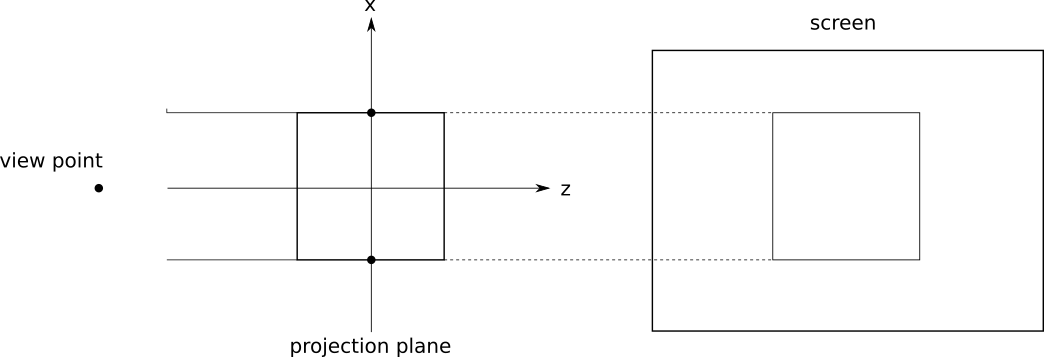
立方体の平行投影
平行投影は透視投影の視点を無限遠に置いたものとしても考えることができる。
\[
x\prime=\lim_{z_0 \to \infty}\frac{x}{1-\frac{z}{z_0}}
\]
\[
y\prime=\lim_{z_0 \to \infty}\frac{y}{1-\frac{z}{z_0}}
\]
よって
\[
x\prime=x\\
y\prime=y
\]
となり、投影後のx座標、y座標は変化しない。