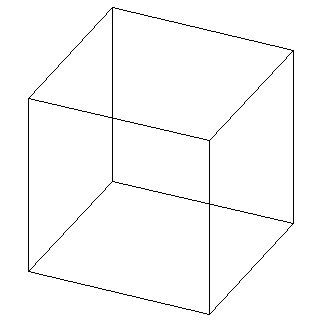
- ワイヤフレーム表示と隠面処理表示 ワイヤフレーム表示は3次元形状を構成する頂点を結んだ稜線だけを表示する形式である。
- 法線ベクトル法 隠面処理において見えない面を消去するにあたり、物体の表面について考えると物体の外側を向いた面だけを表示すれば良い。そして視点から見て反対方向を向いている面は不可視となるため表示は不要となる。
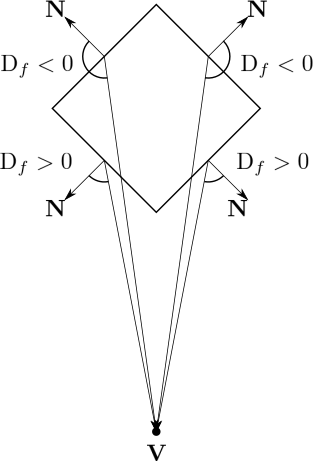
- 表の面と裏の面の判別方法 表の面と裏の面は、面の法線ベクトルと視点と面を結ぶベクトル(視点方向ベクトル)との内積によって判別することができる。 面の法線ベクトルを\(\mathbf{N}\)、視点方向ベクトルを\(\mathbf{V}\)とすると、表の面と裏の面の判別式\(D_f\)は以下のようになる。 \[ D_f=\mathbf{N} \cdot \mathbf{V} \]
- \(D_f>0\Rightarrow\) 表の面
- \(D_f<0\Rightarrow\) 裏の面
- \(D_f=0\Rightarrow\) 視線と平行
- 法線ベクトルの導出 法線ベクトルは3次元形状を構成する面の頂点\(p_i\)を用いて導出できる。
この方法は頂点同士の接続関係の把握のしやすさや表示が高速に行えるなどの利点があるが、
本来見えるはずのないが見えてしまうことにより、表示が煩雑になってしまい面の位置関係の把握や立体の内部と外部の区別がつきにくいなどの問題点もある。
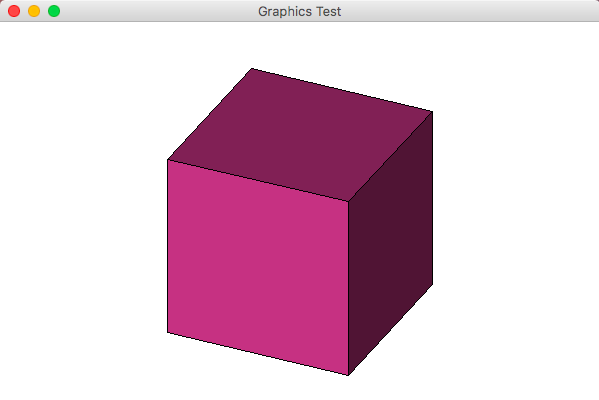
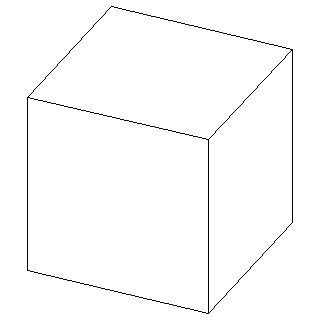
立体の表示において視点から本来見えない面を消去する処理を隠面処理という。 さらに陰影付けをすることでより立体的な表示となる。
 |
 |
 |
| ワイヤフレーム表示 | 隠面処理表示 | 隠面処理+陰影付け |
法線ベクトル法はこのような考えに基づいて隠面処理を行う。すなわち視点から見て裏側となる面を削除、もしくは表示しない方法である。そのため法線ベクトル法はバックフェイスカリング(back-face culling)とも呼ばれる。
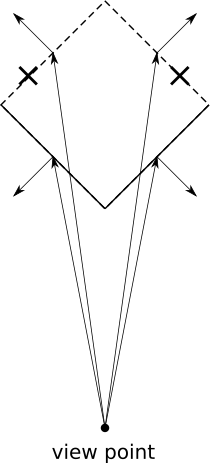
法線ベクトル法の概要
ここでは形状を構成する面を三角形と仮定して法線の導出を行う。
三角形を構成する頂点\(p_0,p_1,p_2\)は面の表側からみて反時計回りに定義されているとする。
右手系の場合、時計回りに定義することで法線は面の表側に向かう。つまり法線ベクトルの向いている方向が面の表になる。
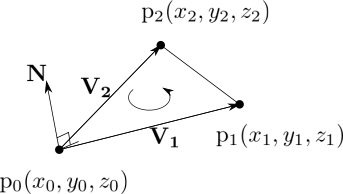 ここで\(p_0,p_1\)からなるベクトル\(\mathbf{V}_1\),\(p_0,p_2\)からなるベクトル\(\mathbf{V}_2\)を導入すると法線ベクトル\(\mathbf{N}\)は\(\mathbf{V}_1\)と\(\mathbf{V}_2\)の外積で表される。
ここで\(p_0,p_1\)からなるベクトル\(\mathbf{V}_1\),\(p_0,p_2\)からなるベクトル\(\mathbf{V}_2\)を導入すると法線ベクトル\(\mathbf{N}\)は\(\mathbf{V}_1\)と\(\mathbf{V}_2\)の外積で表される。すなわち \[ \mathbf{N}=\mathbf{V}_1\times\mathbf{V}_2 \] ただし \[ \mathbf{V}_1=p_1-p_0\\ \mathbf{V}_2=p_2-p_0 \] 従って、法線ベクトル\(\mathbf{N}\)の\(x,y,z\)の各成分\(n_x,n_y,n_z\)は以下のようになる \[ n_x=\mathbf{V}_1y\mathbf{V}_2z-\mathbf{V}_1z\mathbf{V}_2y\\ n_y=\mathbf{V}_1x\mathbf{V}_2z-\mathbf{V}_1z\mathbf{V}_2x\\ n_z=\mathbf{V}_1y\mathbf{V}_2x-\mathbf{V}_1x\mathbf{V}_2y \] もしくは \[ n_x=(y_1-y_0)(z_2-z_0)-(z_1-z_0)(y_2-y_0)\\ n_y=(x_1-x_0)(z_2-z_0)-(z_1-z_0)(x_2-x_0)\\ n_z=(y_1-y_0)(x_2-x_0)-(x_1-x_0)(y_2-y_0)\\ \] 単位法線ベクトル\(\mathbf{\hat{N}}\)は求めた法線ベクトルで正規化することで次のように求められる。 \[ \mathbf{\hat{N}}=\frac{\mathbf{N}}{|\mathbf{N}|} =\frac{\mathbf{N}}{\sqrt{n_x^2+n_y^2+n_z^2}} \] 今回は三角形の面を例に法線ベクトルを導出したが、四角形以上の多角形に対しても任意の3点を選ぶことで同様に導出することができる。
コード(法線ベクトルの導出)