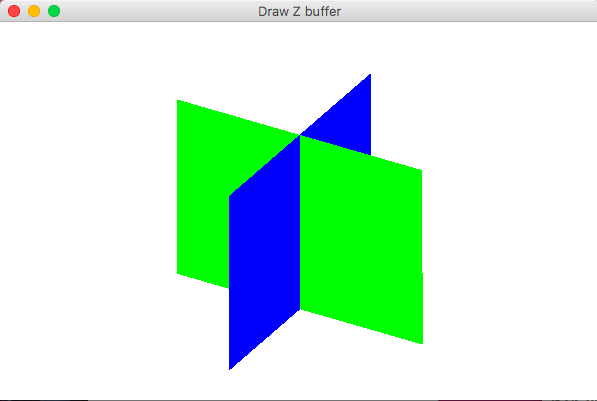
- 隠面処理（Zバッファ法)
- Zバッファ法
Zバッファ法は画素単位で奥行きの判定を行い隠面処理を行う方法で、画像空間アルゴリズムの一種である。同様のアルゴリズムとしてはスキャンライン法、レイトレーシング法がある。
視線の方向をz軸とした場合、これをz軸方向とした場合、これが奥行き(depth)に相当する。そのためこの手法はデプスバッファ法とも呼ばれる。
Zソート法ではポリゴン単位で奥行きの判定を行うため、ポリゴン同士が交差するようなポリゴンの奥行きが交差する場合Zソートは失敗する。Zバッファ法では画素単位の奥行き判定を行うため、このような状況においてもうまく動作する。
- Zバッファ法のアルゴリズム
Zバッファ法では、3次元図形の投影画像の画素情報を格納するフレームバッファを用意する。これに加えて画素の奥行き情報を格納するZバッファあるいはデプスバッファ（奥行きバッファ）を用意する。Zバッファは画素毎の奥行き情報を保持するため、表示する画素と同じ大きさの領域（サイズ）が必要である。
 |
 |
フレームバッファの画素情報 |
Zバッファの画素情報 |
Zバッファ法の基本的な考え方はにはまずZバッファ全体を無限遠（実際には無限遠に相当する値）で初期化しておき、各画素における描画対象のポリゴン上の点までの距離とZバッファの値を比較する深度テスト（またはデプステスト）を行い。距離が小さければフレームバッファの画素値を更新し、同時にZバッファの画素値も更新する。
このため奥行きが大きいポリゴンは奥行きが小さいポリゴンで上書きされるので、視点から見て手前のポリゴンのみ表示されることになる。さらに画素単位で可視判定をするので、ポリゴンの奥行きが交差するような複雑な配置に対しても対応することが可能である。
- Zバッファ法の実装
Zバッファ法の実装方法は様々であるが、今回は内分点を利用した奥行き情報の導出による方法にて実装を行う。
この方法では各ポリゴンに対して、横軸をx、縦軸をyとしてy軸の上から下に走査してポリゴンとの交点を求め、
求めた交点をもとに、二つの交点を結ぶように左右に走査して奥行き情報を判定する。
この交点の導出に内分点を用いる。内分点はx,y,zともに同じ比率になることから交点と同時に奥行き情報も導出することができる。
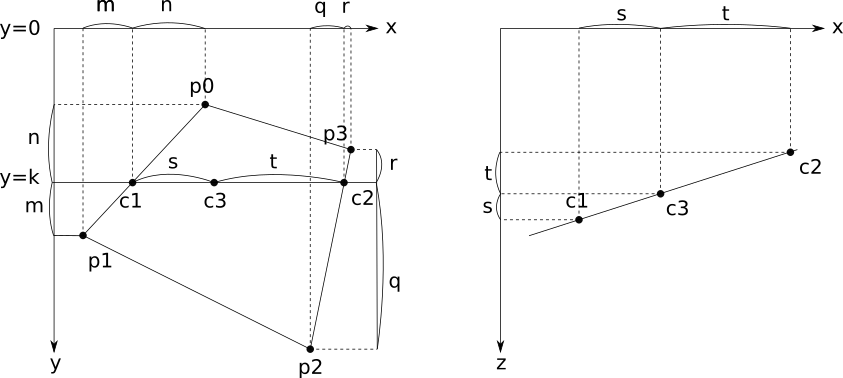交点の座標は内分点を使って以下のように求められる。
\[
c_1=\frac{mp_0+np_1}{m+n}\\
c_2=\frac{qp_3+rp_2}{q+r}\\
c_3=\frac{tc_1+sc_2}{s+t}\\
\]
よってm,nは
\[
m:n=(p_{1y}-k):(k-p_{0y})\\
q:r=(p_{2y}-k):(k-p_{3y})
\]
となり、それぞれの交点c1,c2の座標は
\[
c_{1x}=\frac{(p_{1y}-k)p_{0x}+(k-p_{0y})p_{1x}}{p_{1y}-p_{0y}}\\
c_{1y}=k\\
c_{1z}=\frac{(p_{1y}-k)p_{0z}+(k-p_{0z})p_{1z}}{p_{1y}-p_{0y}}\\
\]
\[
c_{2x}=\frac{(p_{2y}-k)p_{3x}+(k-p_{3y})p_{2x}}{p_{2y}-p_{3y}}\\
c_{2y}=k\\
c_{2z}=\frac{(p_{2y}-k)p_{3z}+(k-p_{3y})p_{2z}}{p_{2y}-p_{3y}}\\
\]
となる。
さらに二つの交点の間の点c3の座標は以下の通りである。
\[
s:t=(c_{3x}-c_{1x}):(c_{2x}-c_{3x})
\]
\[
c_{3x}=\frac{(c_{2x}-c_{3x})c_{1x}+(c_{3x}-c_{1x})c_{2x}}{c_{2x}-c_{1x}}\\
c_{3y}=k\\
c_{3z}=\frac{(c_{2x}-c_{3x})c_{1z}+(c_{3x}-c_{1x})c_{2z}}{c_{2x}-c_{1x}}\\
\]
ここで求まった\(c_{3z}\)をポリゴン上の座標\(c_{3x}\),\(c_{3y}\)でのz値（奥行き）としてデプステストに用いる。
コード
public void zBuffer(Graphics g,Shape shape) {
bg.setColor(Color.white);
bg.fillRect(0, 0, screenW, screenH);
//デプスバッファの初期化
for(int i=0;i<screenH;i++) {
for(int j=0;j<screenW;j++) {
depthBuffer[i][j]=-1e30;
}
}
//頂点データの座標変換
double[][] v=new double[shape.vertices.length][3];
for(int i=0;i<shape.vertices.length;i++) {
v[i]=viewOrtho(shape.vertices[i]);
}
//ポリゴン毎の処理
for(int j=0;j<shape.faces.length;j++) {
double[][] polygon=new double[shape.faces[j].length][3];
for(int i=0;i<shape.faces[j].length;i++) {
polygon[i]=v[shape.faces[j][i]];
}
//面の色を決定
//法線データの座標変換
double[] n=new double[3];
n=viewOrtho(shape.normal[j]);
//重心データの座標変換
double[] fg=new double[3];
fg=viewOrtho(shape.fg[j]);
double[] nv= {
n[0]-o[0],
n[1]-o[1],
n[2]
};
double[] vv= {
fg[0]-vp[0],
fg[1]-vp[1],
fg[2]-vp[2],
};
double dot=nv[0]*vv[0]+nv[1]*vv[1]+nv[2]*vv[2];
Color c=new Color(
(int)clip(dot/vp[2]*255,0,255),
(int)clip(dot/vp[2]*64,0,255),
(int)clip(dot/vp[2]*168,0,255)
);
bg.setColor(c);
if(j==1)
c=Color.blue;
else
c=Color.green;
int top=0;
int bottom=0;
int left=0;
int right=0;
int num=polygon.length;
//y軸の最大値と最小値を求める
for(int i=0;i<num;i++) {
if(polygon[top][1]>polygon[i][1]) {
left=i;
right=i;
top=i;
}
if(polygon[bottom][1]<polygon[i][1]) {
bottom=i;
}
}
//yを上から走査する
for(double y=polygon[top][1];y<polygon[bottom][1];y+=0.1) {
if(y<0||y>screenH)continue;
//左側の線分の終端を超えたら次の直線を走査（反時計回り）
if(polygon[(left+1)%num][1]<=y) {
left=(left+1)%num;
}
//右側の線分の終端を超えたら次の直線を走査（時計周り）
if(polygon[(right-1+polygon.length)%polygon.length][1]<=y) {
right=(right-1+polygon.length)%polygon.length;
}
//直線の内分点を求める
double[] p0=polygon[right];
double[] p1=polygon[left];
double[] p2=polygon[(left+1)%polygon.length];
double[] p3=polygon[(right-1+polygon.length)%polygon.length];
double[] start=new double[3];
start[0]=((p2[1]-y)*p1[0]+(y-p1[1])*p2[0])/(p2[1]-p1[1]);
start[1]=y;
start[2]=((p2[1]-y)*p1[2]+(y-p1[1])*p2[2])/(p2[1]-p1[1]);
double[] end=new double[3];
end[0]=((p3[1]-y)*p0[0]+(y-p0[1])*p3[0])/(p3[1]-p0[1]);
end[1]=y;
end[2]=((p3[1]-y)*p0[2]+(y-p0[1])*p3[2])/(p3[1]-p0[1]);
//始点と終点が入れ替わっていたら交換
if(start[0]>end[0]) {
double[] w=start;
start=end;
end=w;
}
//深度テスト
for(double x=start[0];x<end[0];x++) {
if(x<0||x>screenW)continue;
if(y<0||y>screenH)continue;
double[] q=new double[3];
q[0]=x;
q[1]=y;
q[2]=((end[0]-x)*start[2]+(x-start[0])*end[2])/(end[0]-start[0]);
if(depthBuffer[(int)y][(int)x]<q[2]) {
buffer.setRGB((int)x, (int)y, c.getRGB());
depthBuffer[(int)y][(int)x]=q[2];
buffer.setRGB((int)x, (int)y, c.getRGB());
}
}
}
}
g.drawImage(buffer,0,0,null);
}
