- Bスプライン曲線 Bスプライン曲線は複数の制御点とノット列(ノットベクトル:knot vector)から生成されるなめらかな曲線で実験データなどの 曲線割り当て、CAD、コンピュータグラフィックスなどの領域で利用されている。
- 制御点の一部を変更しても曲線全体に影響しない(局所性)
- 曲線は始点、終点も含み、必ず制御点を通るとは限らない(基本的には通らない)
- 曲線の形は制御点の位置、ノットベクトルの値、次数で決まる
- 制御点が重なると尖った形状になる
- Bスプライン曲線の定義式 \(m\)個の制御点\(P_i\)と\(k\)個のノットベクトル\(t_i\)によって定義されたn次のBスプライン曲線\(S(t)\)は以下の式で定義される。
- 基底関数 基底関数はノットベクトルの関数になっており、以下の様に定義される。(de Boor Coxの漸化式) \[ b^{0}_{j}(t)= \left\{ \begin{array}{1} 1 & (t_j \leq t \lt t_{j+1})\\ 0 & otherwise \end{array} \right. \] \[ b^{n}_{j}(t)=\frac{t-t_j}{t_{j+n}-t_j}b^{n-1}_{j}(t)+\frac{t_{j+n+1}-t}{t_{j+n+1}-t_{j+1}}b^{n-1}_{j+1}(t) \] 生成する曲線の次数によって異なる次数の基底関数を使う。
- ノットベクトル ノットベクトルはノット(knot:結び目)と呼ばれる実数値が複数集まって構成されるベクトルのことをいう
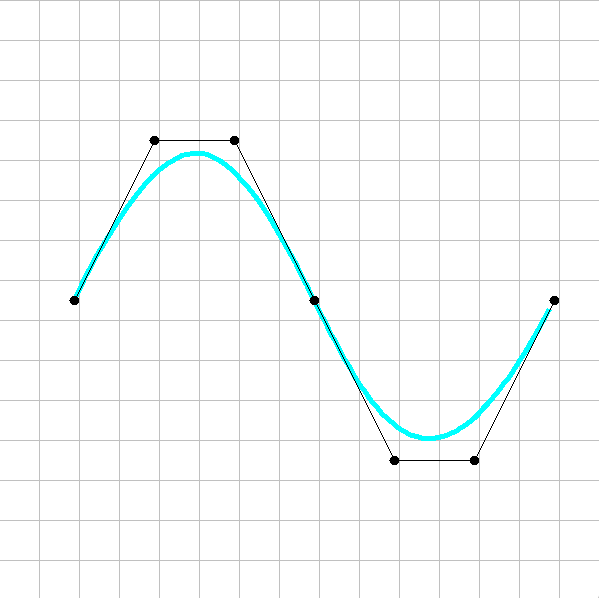
- サンプルプログラムの概要 Bスプライン曲線を描画するプログラムで、制御点をマウスでドラッグすると制御点を移動させてある程度の曲線の制御が可能。
Bスプライン曲線の名前はBasis splineの省略系で曲線生成に利用する基底(basis)関数に由来する。
曲線の特徴としては
このときの接続の度合いを決めるパラメータを設定するのがノット列である。(ノットの数\(k\)は制御点数\(m\)+次数\(n\)+1になる)

3次Bスプライン曲線
7個の制御点(黒丸)と 10個のノット列で生成されたBスプライン曲線
すべて3次曲線で構成されている
7個の制御点(黒丸)と 10個のノット列で生成されたBスプライン曲線
すべて3次曲線で構成されている
\[S(t)=\sum^{m-1}_{i=0}b^{n}_{i}(t)P_i\] ここで\(b^{n}_{i}(t)\)は基底関数(basis function)で制御点に対して重み付けを行うことで曲線を生成する。
今のノットベクトル\(t\)について、0から1ずつ増加する \[t=[0,1,2,3,\cdots t_j]\] を\(j=0\),\(n=0\)のときにについて。 \[ b^{0}_{0}(t)= \left\{ \begin{array}{1} 1 & (0 \leq t \lt 1)\\ 0 & otherwise \end{array} \right. \] とかけるのでグラフは以下の様になる
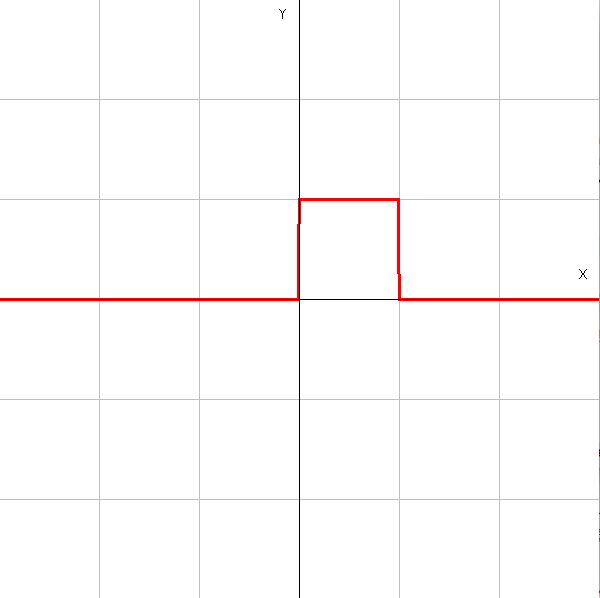
0次基底関数\(b^{0}_{0}\)
次に\(j=0\),\(n=1\)のときにについて。
\[
\begin{eqnarray}
b^{1}_{0}(t)&=&\frac{t-t_0}{t_{1}-t_0}b^{0}_{0}(t)+\frac{t_{2}-t}{t_{2}-t_{1}}b^{0}_{1}(t)\\
&=&tb^{0}_{0}(t)+(2-t)b^{0}_{1}(t)
\end{eqnarray}
\]
となる。ここで
\[
b^{0}_{1}(t)=
\left\{
\begin{array}{1}
1 & (1 \leq t \lt 2)\\
0 & otherwise
\end{array}
\right.
\]
より
\[
b^{1}_{0}(t)=
\left\{
\begin{array}{1}
t & (0 \leq t \lt 1)\\
2-t & (1 \leq t \lt 2)\\
0 & otherwise
\end{array}
\right.
\]
とかけるのでグラフは以下の様になる
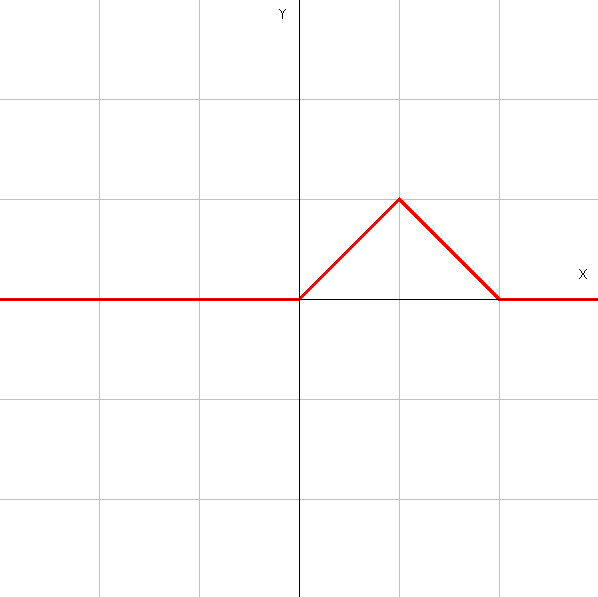
1次基底関数\(b^{1}_{0}\)
次に\(j=0\),\(n=2\)のときにについて。
\[
\begin{eqnarray}
b^{2}_{0}(t)&=&\frac{t-t_0}{t_{2}-t_0}b^{1}_{0}(t)+\frac{t_{3}-t}{t_{3}-t_{1}}b^{1}_{1}(t)\\
&=&\frac{t}{2}b^{1}_{0}(t)+\frac{(3-t)}{2}b^{1}_{1}(t)
\end{eqnarray}
\]
となる。ここで\(b^{1}_{1}(t)\)が未知なので、これについて解く
\[
\begin{eqnarray}
b^{1}_{1}(t)&=&\frac{t-t_1}{t_{2}-t_1}b^{0}_{1}(t)+\frac{t_{3}-t}{t_{3}-t_{2}}b^{0}_{2}(t)\\
&=&(t-1)b^{0}_{0}(t)+(3-t)b^{0}_{1}(t)
\end{eqnarray}
\]
となる。ここで
\[
b^{0}_{2}(t)=
\left\{
\begin{array}{1}
1 & (2 \leq t \lt 3)\\
0 & otherwise
\end{array}
\right.
\]
より
\[
b^{1}_{1}(t)=
\left\{
\begin{array}{1}
t-1 & (1 \leq t \lt 2)\\
3-t & (2 \leq t \lt 3)\\
0 & otherwise
\end{array}
\right.
\]
と求められ、既知の関数のみとなった。
これを先ほどの式に代入して、各区間について考える\(0\leq t\lt1\)のとき \[ b^{2}_{0}=\frac{t}{2}\cdot t+\frac{3-t}{2}\cdot 0=\frac{t^2}{2} \] \(1\leq t\lt2\)のとき \[ b^{2}_{0}=\frac{t}{2}\cdot (2-t)+\frac{3-t}{2}\cdot(t-1)=\frac{-2t^2+6t-3}{2} \] \(2\leq t\lt3\)のとき \[ b^{2}_{0}=\frac{t}{2}\cdot 0+\frac{3-t}{2}\cdot(3-t)=\frac{t^2-6t+9}{2} \] 以上をまとめると \[ b^{2}_{0}(t)= \left\{ \begin{array}{1} \frac{t^2}{2} & (0 \leq t \lt 1)\\ \frac{-2t^2+6t-3}{2} & (1 \leq t \lt 2)\\ \frac{t^2-6t+9}{2} & (2 \leq t \lt 3)\\ 0 & otherwise \end{array} \right. \] とかけるのでグラフは以下の様になる
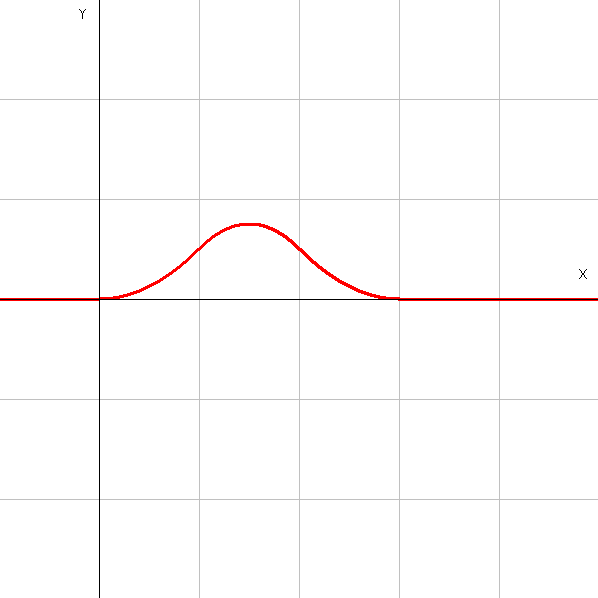
2次基底関数\(b^{2}_{0}\)
次に\(j=0\),\(n=3\)のときは計算は省略するが同じ様に計算すると。 \[ b^{2}_{0}(t)= \left\{ \begin{array}{1} \frac{t^3}{6} & (0 \leq t \lt 1)\\ \frac{-3t^3+12t^2-12t+4}{6} & (1 \leq t \lt 2)\\ \frac{3t^3-24t^2+60t-44}{6} & (2 \leq t \lt 3)\\ \frac{(4-t)^3}{6} & (3 \leq t \lt 4)\\ 0 & otherwise \end{array} \right. \] とかけるのでグラフは以下の様になる
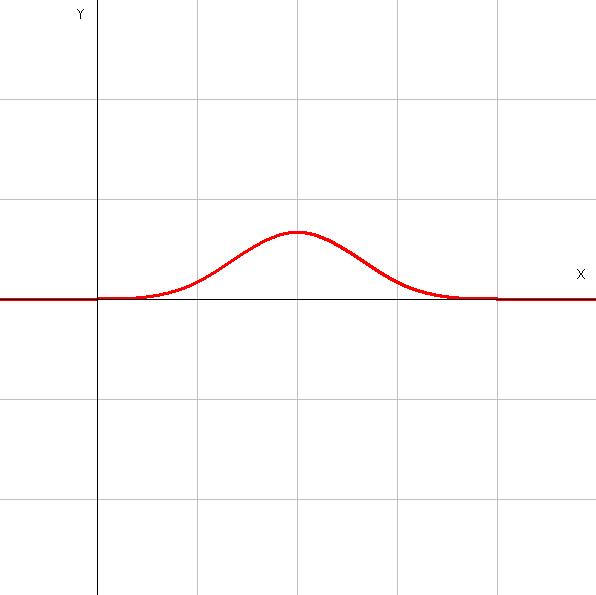
3次基底関数\(b^{3}_{0}\)
0次の場合はの一定の区間のみ値を持ちそれ以外では0のステップ関数になっているが、 1次以上では次数に対応した関数で区間外に近くにつれて0に近く様な形の関数になっている。 \(j=0\)以外のノットベクトルは以下の様に区間を重複しながら、曲線の全ての区間をカバーしている。 基底関数は離れた区間では0になっており、影響を及ぼさないことがわかる。これがBスプライン曲線のもつ局所性を示している。

0次基底関数\(b^{0}_{j}\)
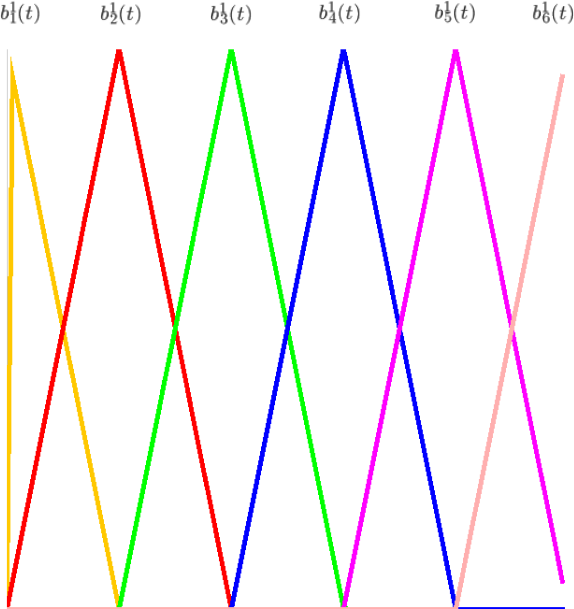
1次基底関数\(b^{1}_{j}\)
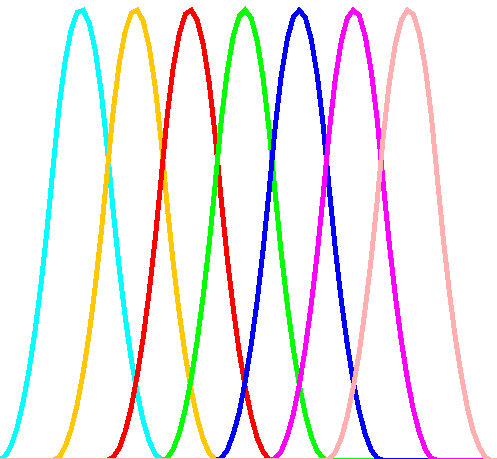
2次基底関数\(b^{2}_{j}\)
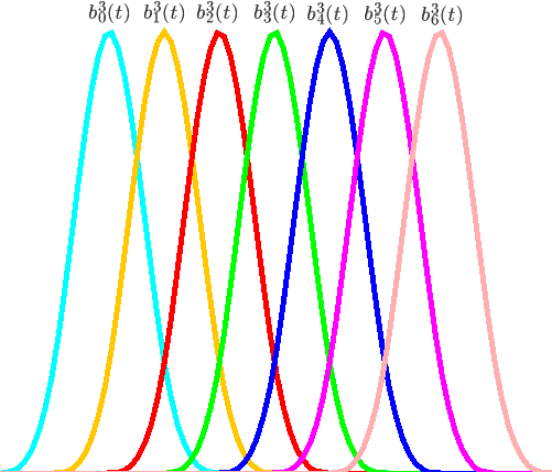
3次基底関数\(b^{3}_{j}\)
ノットの数値が曲線に与えるのはノットベクトル内の相対値であり、絶対的な数値ではないことに注意。
Bスプライン曲線では一様ノットベクトルと開一様ノットベクトルがよく使われる。
一様ノットベクトルはベクトルないの数値が等間隔に上昇するものをいう。
先ほどの例の様に0から1ずつ等間隔に増加するものは一様ノットベクトルである。
例 \[ [0,1,2,3,4,5,6,7,8,9]\\ [0,0.125,0.25,0,375,0.5.0.625,0.75,0.875,1] \] Bスプライン曲線の特徴として、制御点を通る保証がないというものがあるが、始点終点は必ず通したい場合もある。 そういった場合には開一様ノットベクトルを利用する。 次数\(+1\)回、始点と終点の値を重ねることで始点と終点を通るような曲線を生成することが可能である。
例
次数が3の時 \[ [0,0,0,0,1,2,3,3,3,3] \] 次数が2の時 \[ [0,0,0,0.25,0.5.0.75,1,1,1] \]
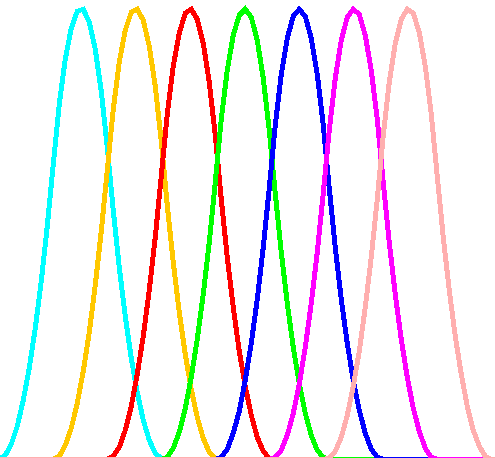
一様ノットベクトルにより生成される基底関数
各区間の関数の形状が一定
各区間の関数の形状が一定
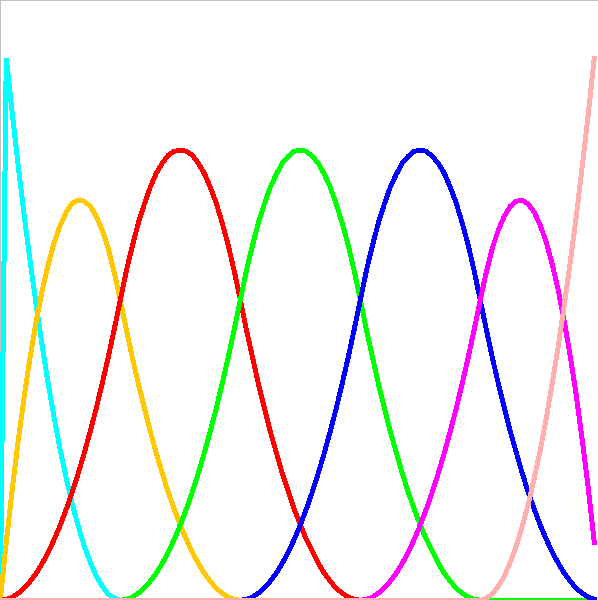
開一様ノットベクトルにより生成される基底関数
各区間の関数の形状が異なる
各区間の関数の形状が異なる
プログラムでの実装
制御点数は固定で7つ。左端の制御点以外の六つの制御点を操作可能。
ノットベクトルは開一様ノットベクトルで0から1までの設定で自動生成される。
次数はメニューから2次から5次までを選択できる。
制御点同士を重ねる様に移動すると制御点が融合される。
メニューから制御点を初期状態に戻すことができる。
プログラムのコア部分を掲載する。詳細はソースファイルを参照のこと。
 サンプルプログラム(実行可能JARファイル)
サンプルプログラム(実行可能JARファイル)