Javaプログラミング

有限要素法による構造解析

• 有限要素法（ゆうげんようそほう、英語: Finite Element Method, FEM）は数値解析手法の一つ
• 解析する領域全体を要素と呼ばれる小領域に分割し解析
• 要素ごとの挙動（関係）を方程式で記述してモデル化
• 要素ごとのモデルを全体の要素について重ね合わせることで、領域全体をモデル化
• モデルの線型性を仮定しているので、静止状態で力の釣り合い状態にある剛体の微小変形が解析対象
• 粘土のような塑性変形、ゴムのような大変形を伴うモデルには適さない

１次元有限要素法

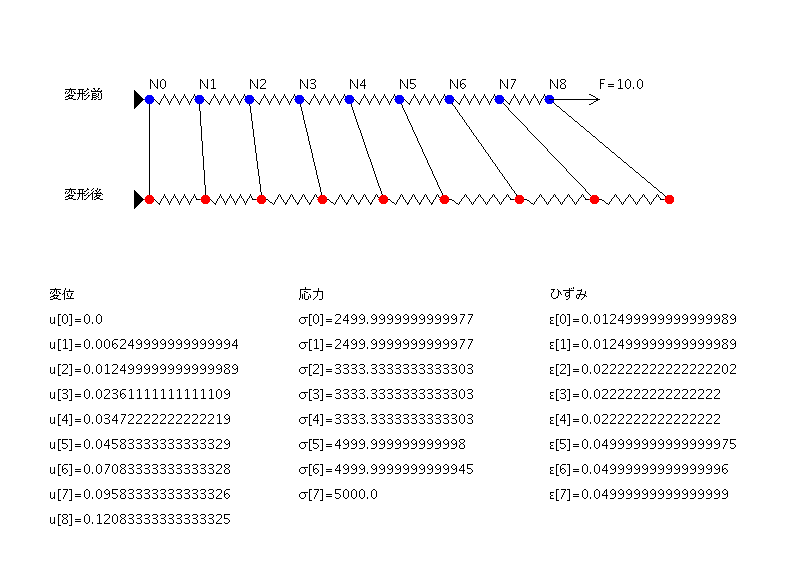
• １次元有限要素法による構造解析
• 有限要素法による構造解析の手順
• 要素構成マトリクスの導出
構造解析の基本式から要素構成マトリクスを作成する
• 全体剛性マトリクスの導出
要素構成マトリクスを重ね合わせて全体剛性マトリクスを作成する
• 境界条件の設定
境界条件として拘束条件を設定する
• 連立方程式の構築
全体構成マトリクス、変位ベクトル、荷重ベクトルを構造解析の基本式に基づいて、連立方程式を立てる
• 変位ベクトルの導出
連立方程式をを解いて、変位ベクトルを求める
• ひずみと応力の導出
得られた変位ベクトルから各要素のひずみと応力を求める
• 構造解析の基本式
有限要素法における構造解析では基本的にフックの法則を用いて要素の挙動をモデル化する \[ ku=f \] ただしkはバネ定数、uは変位、fは荷重を表す。
有限要素法では一般的にkはマトリクス（行列）、u,fはベクトルになる
すなわち以下のように表される \[ K\vec{u}=\vec{f} \]
• 剛性マトリクス
構造解析の基本式のうち、Kに相当するマトリクスを剛性マトリクスと呼ぶ
要素１つについての関係を表すモデルを記述したマトリクスを要素剛性マトリクス、
解析領域全体に重ね合わせたモデルを記述したマトリクスを全体剛性マトリクスと呼ぶ

• 変位ベクトル
構造解析の基本式のうち、uに相当するベクトルを変位ベクトルとよぶ
要素の境界部分を構成するノード（節点）の変位を表す
多くの場合、未知数として扱い解析ではこの値を求める 拘束条件の入力に使うこともある。
• 荷重ベクトル
構造解析の基本式のうち、fに相当するベクトルを荷重ベクトルとよぶ
シミュレーションにおいて荷重条件を設定する場合に用いる。
• 要素構成マトリクスの導出
• 静的釣り合いの条件式
要素が釣り合いの状態にあり、静止している時、要素に加わっている荷重の総和は0である必要がある。 ２節点から構成されるモデル（ロッド要素）のおいて両端にかかる荷重をf₁,f₂とすると以下の式が成立する。 \[ f_1+f_2=0 \] もしくは \[ f_2=-f_1 \]
• ひずみと変位の関係式
ひずみとは長さの変化量をもとの長さで割ったもの。
ひずみをε、節点１、節点２の変位をそれぞれu₁,u₂、元の長さをLとすると以下の関係式が成立する \[ \epsilon=\frac{u_2-u_1}{L} \]
• 応力とひずみの関係式
応力と歪みの関係式はバネ係数をヤング率Eとして、応力をσ、歪みをεとしてフックの法則を使って以下のように与えられる \[ \sigma=E\epsilon \]
• 力と応力の関係式
断面積をAとする節点にかかる力とf₁、f₂と応力には以下の関係が成り立つ \[ f_1=-\sigma A \] \[ f_2=\sigma A \]
• 変位と力の関係式
応力と歪みの関係式、力と応力の関係式より、f₁、f₂は以下のように書ける \[f_1=-E \epsilon A\] \[f_2=E \epsilon A\] さらに歪みと変位の関係式より、変位と力の関係式は以下のようになる \[f_1=-\frac{EA(u_2-u_1)}{L}\] \[f_2=\frac{EA(u_2-u_1)}{L}\] 式を展開して \[f_1=\frac{EA}{L}u_1-\frac{EA}{L}u_2\] \[f_2=-\frac{EA}{L}u_1+\frac{EA}{L}u_2\] 行列の形で表すと以下のようになる。 \[ \begin{bmatrix} \frac{EA}{L} & -\frac{EA}{L}\\ -\frac{EA}{L} & \frac{EA}{L} \end{bmatrix} \begin{bmatrix} u_1\\ u_2 \end{bmatrix} = \begin{bmatrix} f_1\\ f_2 \end{bmatrix} \] ここで \[ K= \begin{bmatrix} \frac{EA}{L} & -\frac{EA}{L}\\ -\frac{EA}{L} & \frac{EA}{L} \end{bmatrix} \] とおくと、これが要素剛性マトリクスとなる。

• 全体剛性マトリクスの導出
要素剛性マトリクスを重ね合せることで全体剛性マトリクスを導出する 全体剛性マトリクスとして要素剛性マトリクスを２つ連結したケースを考える すなわち連結した要素剛性マトリクスをK_a、K_bとして、それぞれ以下のようにおく \[ K_a= \begin{bmatrix} \frac{E_a A_a}{L_a} & -\frac{E_a A_a}{L_a}\\ -\frac{E_a A_a}{L_a} & \frac{E_a A_a}{L_a} \end{bmatrix} \] \[ K_b= \begin{bmatrix} \frac{E_b A_b}{L_b} & -\frac{E_b A_b}{L_b}\\ -\frac{E_b A_b}{L_b} & \frac{E_b A_b}{L_b} \end{bmatrix} \] これら２つの要素剛性マトリクスを重ね合せると全体剛性マトリクスKは以下のようになる \[ K= \begin{bmatrix} \frac{E_a A_a}{L_a} & -\frac{E_a A_a}{L_a} & 0\\ -\frac{E_a A_a}{L_a} & \frac{E_a A_a}{L_a} + \frac{E_b A_b}{L_b} & -\frac{E_b A_b}{L_b}\\ 0 & -\frac{E_b A_b}{L_b} & \frac{E_b A_b}{L_b} \end{bmatrix} \]
• 境界条件の設定
要素の一端を固定した状態を考える u₁,u₂,u₃のうち、u₁を固定すると、u₁の変位が0になる。 すなわち変位ベクトルは以下のようになる \[ \vec{u}= \begin{bmatrix} 0\\ u_2\\ u_3 \end{bmatrix} \] また荷重条件としてf₃にのみに荷重Fを加えると荷重ベクトルは以下のようになる \[ \vec{f}= \begin{bmatrix} 0\\ 0\\ F \end{bmatrix} \]
• 連立方程式の構築
以上により構造解析の基本式に必要な剛性マトリクス、変位ベクトル、荷重ベクトルが求まったので、
構造解析の基本式にあてはめて変位ベクトルを未知数とする連立方程式を構築する。 \[ \begin{bmatrix} \frac{E_a A_a}{L_a} & -\frac{E_a A_a}{L_a} & 0\\ -\frac{E_a A_a}{L_a} & \frac{E_a A_a}{L_a} + \frac{E_b A_b}{L_b} & -\frac{E_b A_b}{L_b}\\ 0 & -\frac{E_b A_b}{L_b} & \frac{E_b A_b}{L_b} \end{bmatrix} \begin{bmatrix} 0\\ u_2\\ u_3 \end{bmatrix} ＝ \begin{bmatrix} 0\\ 0\\ F \end{bmatrix} \] ここでu₁は既知かつ0なので \[ \begin{bmatrix} 0 & 0 & 0\\ 0 & \frac{E_a A_a}{L_a} + \frac{E_b A_b}{L_b} & -\frac{E_b A_b}{L_b}\\ 0 & -\frac{E_b A_b}{L_b} & \frac{E_b A_b}{L_b} \end{bmatrix} \begin{bmatrix} 0\\ u_2\\ u_3 \end{bmatrix} ＝ \begin{bmatrix} 0\\ 0\\ F \end{bmatrix} \] となり、最終的に解くべき連立方程式は以下のようになる \[ \begin{bmatrix} \frac{E_a A_a}{L_a} + \frac{E_b A_b}{L_b} & -\frac{E_b A_b}{L_b}\\ -\frac{E_b A_b}{L_b} & \frac{E_b A_b}{L_b} \end{bmatrix} \begin{bmatrix} u_2\\ u_3 \end{bmatrix} ＝ \begin{bmatrix} 0\\ F \end{bmatrix} \]
• 連立方程式の解の導出
得られた式をガウス法などによって解き、未知数である変位ベクトルuを得る。
• ひずみと応力の導出
要素aのひずみ \[ \epsilon_a=\frac{u_1-u_0}{L_a} \] 要素aの応力 \[ \sigma_a=E\epsilon_a=E\frac{u_1-u_0}{L_a} \] 要素bのひずみ \[ \epsilon_b=\frac{u_2-u_1}{L_b} \] 要素bの応力 \[ \sigma_b=E\epsilon_b=E\frac{u_2-u_1}{L_b} \]

２次元有限要素法