- 連立方程式
連立方程式は線型代数学の1大分野であり、線型代数学は連立方程式の解法と性質を知るために発展してきたものでもある。
応用範囲も非常に広く工学をはじめとした様々な分野で利用されている。
変数の少ない2変数の2元一次連立方程式や3変数の3元一次連立方程式程度であれば手計算でも比較的容易に解を得ることができるが、
工学などの応用では数百や数万変数の連立方程式を扱うこともまれではなく、コンピュータを使った効率的な解法が望まれる。
- 連立方程式の解法
以下に示す様な3変数3元一次連立方程式を解くことを考える
\[
\left\{
\begin{array}{1}
6x+5y+4z=8 &(1)\\
12x+13y+10z=16 &(2)\\
18x+21y+17z=27 &(3)\\
\end{array}
\right.
\]
\((1)\times 2-(2)\),\((1)\times 3-(3)\)
\[
\left\{
\begin{array}{1}
6x+5y+4z=8 &(1)\\
3y+2z=0 &(2)\\
6y+5z=3 &(3)\\
\end{array}
\right.
\]
\((2)\times 2-(3)\)
\[
\left\{
\begin{array}{1}
6x+5y+4z=8 &(1)\\
3y+2z=0 &(2)\\
z=3 &(3)\\
\end{array}
\right.
\]
\((3)\)を\((2)\)に代入して
\[
\left\{
\begin{array}{1}
6x+5y+4z=8 &(1)\\
y=−2 &(2)\\
z=3 &(3)\\
\end{array}
\right.
\]
\((2)\),\((3)\)を\((1)\)に代入して
\[
\left\{
\begin{array}{1}
x=1 &(1)\\
y=-2 &(2)\\
z=3 &(3)\\
\end{array}
\right.
\]
\[
\therefore x=1,y=-2,z=3
\]
様々な解法が存在するがこれが一般的な解法の1つである。
この解法の特徴はある変数が決まったら、その変数を他の式に代入して他の変数も順次求めてゆくと言うところにある。
この方法を消去法(あるいはガウスの消去法という)
- 連立方程式と拡大係数行列
先程と同じ連立方程式を行列を使って解くことを考える
\[
\left\{
\begin{array}{1}
6x+5y+4z=8\\
12x+13y+10z=16\\
18x+21y+17z=27\\
\end{array}
\right.
\]
この様な連立方程式が与えられた場合、行列の積を使って次の様に書き換えられる
\[
\left[
\begin{array}{1}
6 & 5 & 4\\
12 &13 &10\\
18 &21 &17\
\end{array}
\right]
\left[
\begin{array}{1}
x\\
y\\
z\\
\end{array}
\right]
=
\left[
\begin{array}{1}
8\\
16\\
27\\
\end{array}
\right]
\]
この時、数字のみの行列(左辺の係数と右辺の定数)のみを組み合わせて次の様に書き換えることができる。
\[
\left[
\begin{array}{ccc|c}
6 & 5 & 4 & 8\\
12 &13 &10 &16\\
18 &21 &17 &27\\
\end{array}
\right]
\]
この様な行列を拡大係数行列と言う。
文字を使って一般化すると
\[
\left\{
\begin{array}{1}
a_{11}x+a_{12}y+a_{13}z=b_1\\
a_{21}x+a_{22}y+a_{23}z=b_2\\
a_{31}x+a_{32}y+a_{33}z=b_3\\
\end{array}
\right.
\]
で与えられた連立方程式は次の様な拡大係数行列で書き換えられる。
\[
\left[
\begin{array}{ccc|c}
a_{11} &a_{12} &a_{13} &b_{1}\\
a_{21} &a_{22} &a_{23} &b_{2}\\
a_{31} &a_{32} &a_{33} &b_{3}\\
\end{array}
\right]
\]
さらに一般化して、n変数のn元一次連立方程式について
\[
\left\{
\begin{array}{1}
a_{11}x_{1} + a_{12}x_{2} + \cdots + a_{1n}x_{n} =b_{1}\\
a_{21}x_{1} + a_{22}x_{2} + \cdots + a_{2n}x_{n} =b_{2}\\
\vdots \\
a_{n1}x_{1} + a_{n2}x_{2} + \cdots = a_{nn}x_{n} =b_{n}
\end{array}
\right.
\]
やはり、次の様に書き換えることができる。
\[
\left[
\begin{array}{cccc|c}
a_{11} &a_{12} & \cdots &a_{13} &b_{1}\\
a_{21} &a_{22} & \cdots &a_{23} &b_{2}\\
\vdots & \vdots & \ddots & \vdots & \vdots \\
a_{31} &a_{32} & \cdots &a_{33} &b_{3}\\
\end{array}
\right]
\]
- 拡大係数行列と行基本変形
拡大係数行列において縦線の左側を係数行列、右側を定数項ベクトルと言う。
この行列に対しては通常連立方程式に対して行う三つの操作
- 2つの行を入れ替える
- ある行に0でない定数をかける
- ある行の定数倍を他の行に加える
これらの操作を行基本変形という。
拡大係数行列において行基本変形を行う前と行った後は同値である。
すなわち以下が成り立つ
- 2つの行を入れ替える
\[
\left[
\begin{array}{cccc|c}
\vdots & \vdots & \cdots &\vdots &\vdots\\
a_{i1} &a_{i2} & \cdots &a_{in} &b_{i}\\
\vdots & \vdots & \ddots & \vdots & \vdots \\
a_{j1} &a_{j2} & \cdots &a_{jn} &b_{j}\\
\vdots & \vdots & \cdots &\vdots &\vdots\\
\end{array}
\right]
=
\left[
\begin{array}{cccc|c}
\vdots & \vdots & \cdots &\vdots &\vdots\\
a_{j1} &a_{j2} & \cdots &a_{jn} &b_{j}\\
\vdots & \vdots & \ddots & \vdots & \vdots \\
a_{i1} &a_{i2} & \cdots &a_{in} &b_{i}\\
\vdots & \vdots & \cdots &\vdots &\vdots\\
\end{array}
\right]
\]
- ある行に0でない定数をかける
\[
\left[
\begin{array}{cccc|c}
\vdots & \vdots & \cdots &\vdots &\vdots\\
a_{i1} &a_{i2} & \cdots &a_{in} &b_{i}\\
\vdots & \vdots & \cdots &\vdots &\vdots\\
\end{array}
\right]
=
\left[
\begin{array}{cccc|c}
\vdots & \vdots & \cdots &\vdots &\vdots\\
ca_{i1} &ca_{i2} & \cdots &ca_{in} &cb_{i}\\
\vdots & \vdots & \cdots &\vdots &\vdots\\
\end{array}
\right]
\ \ \ (c \neq 0)
\]
- ある行の定数倍を他の行に加える
\[
\left[
\begin{array}{cccc|c}
\vdots & \vdots & \cdots &\vdots &\vdots\\
a_{i1} &a_{i2} & \cdots &a_{in} &b_{i}\\
\vdots & \vdots & \ddots & \vdots & \vdots \\
a_{j1} &a_{j2} & \cdots &a_{jn} &b_{j}\\
\vdots & \vdots & \cdots &\vdots &\vdots\\
\end{array}
\right]
=
\left[
\begin{array}{cccc|c}
\vdots & \vdots & \cdots &\vdots &\vdots\\
a_{i1} &a_{i2} & \cdots &a_{in} &b_{i}\\
\vdots & \vdots & \ddots & \vdots & \vdots \\
ca_{i1}+a_{j1} &ca_{i2}+a_{j2} & \cdots &ca_{in}+a_{jn} &cb_{i}+b_{j}\\
\vdots & \vdots & \cdots &\vdots &\vdots\\
\end{array}
\right]
\ \ \ (c \neq 0)
\]
- 拡大係数行列を用いた解法
\[
\left[
\begin{array}{ccc|c}
6 & 5 & 4 & 8\\
12 &13 &10 &16\\
18 &21 &17 &27\\
\end{array}
\right]
\]
1行目�に−2をかけて2行目に加える
1行目に−3をかけて3行目に加える
\[
\left[
\begin{array}{ccc|c}
6 & 5 & 4 & 8\\
0 & 3 & 2 & 0\\
0 & 6 & 5 & 3\\
\end{array}
\right]
\]
2行目に−2をかけて3行目に加える
\[
\left[
\begin{array}{ccc|c}
6 & 5 & 4 & 8\\
0 & 3 & 2 & 0\\
0 & 0 & 1 & 3\\
\end{array}
\right]
\]
3行目に−2をかけて2行目に加える
\[
\left[
\begin{array}{ccc|c}
6 & 5 & 4 & 8\\
0 & 3 & 0 & -6\\
0 & 0 & 1 & 3\\
\end{array}
\right]
\]
2行目に1/3をかける
\[
\left[
\begin{array}{ccc|c}
6 & 5 & 4 & 8\\
0 & 1 & 0 & -2\\
0 & 0 & 1 & 3\\
\end{array}
\right]
\]
2行目に−5をかけて1行目に加える
3行目に−4をかけて1行目に加える
\[
\left[
\begin{array}{ccc|c}
6 & 0 & 0 & 6\\
0 & 1 & 0 & -2\\
0 & 0 & 1 & 3\\
\end{array}
\right]
\]
1行目に1/6をかける
\[
\left[
\begin{array}{ccc|c}
1 & 0 & 0 & 1\\
0 & 1 & 0 & -2\\
0 & 0 & 1 & 3\\
\end{array}
\right]
\]
係数行列の対角成分、すなわち\(a_{ii}\)\((i=1\dots3)\)が全て1でそれ以外が全て0であるとき、
連立方程式が解けたことになる。
確認のためもう一度行列の積の形にもどすと
\[
\left[
\begin{array}{1}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1\
\end{array}
\right]
\left[
\begin{array}{1}
x\\
y\\
z\\
\end{array}
\right]
=
\left[
\begin{array}{1}
1\\
-2\\
3\\
\end{array}
\right]
\]
左辺を計算すると
\[
\left[
\begin{array}{1}
x\\
y\\
z\\
\end{array}
\right]
=
\left[
\begin{array}{1}
1\\
-2\\
3\\
\end{array}
\right]
\]
\[
\therefore x=1,y=-2,z=3
\]
となり解が得られていることがわかる。
この方法は行基本変形のみを用いて、係数行列の対角成分を全て1にすることにある。
この方法を掃出し法(あるいはガウス=ジョルダン法)という。
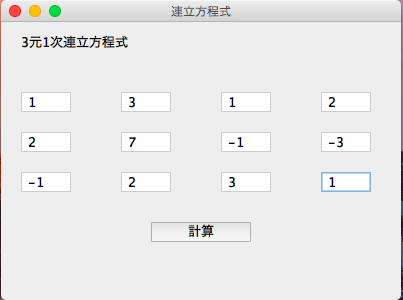
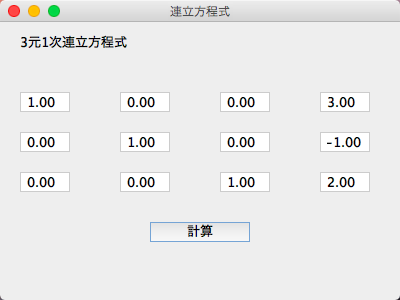
・おまけ
3元1次連立方程式を解くGUIアプリケーション。
係数行列と定数項ベクトルを入れて計算ボタンを押すと計算実行。
係数行列部分の対角成分に1を残しておけば2元以下も解くことが可能。
入力チェック、エラーチェック等未実装。コードは殴り書きレベル。
 サンプルプログラム(実行可能JARファイル)
サンプルプログラム(実行可能JARファイル)
サンプルコード

 サンプルプログラム(実行可能JARファイル)
サンプルプログラム(実行可能JARファイル)