テイラー展開（Taylor expansion）

• テイラー級数とテイラー展開
• テイラー級数やテイラー展開の考えは数学や物理、工学などの幅広い分野の問題で頻繁に利用されている。
  テイラー展開は任意の関数を多項式の線形結合（係数を掛けたものの和）の無限和、つまり級数に展開することを言う。
  このとき展開される級数のことをテイラー級数といい、以下の形で表される。
  \[f(x)=\sum^\infty_{k=0}\frac{f^{(k)}(a)}{k!}(x-a)^k\]
• テイラー展開とマクローリン展開
• 任意の関数 \(f(x)\) について以下の様に記述できるとする。 \[f(x)=a_0+a_1x+a_2x^2+ \cdots +a_nx^n + \cdots\] ここで\(f(x)\)は無限回微分可能だとして\(x\)で\(n\)回微分する。 \[f'(x)= a_1+2a_2x+3a_3x^2+ \cdots +na_nx^{n-1}+\cdots\] \[f''(x)= 2a_2+2\cdot3a_3x+3\cdot4a_4x^2+ \cdots +n(n-1)a_nx^{n-2}+\cdots\] \[f'''(x)= 2\cdot3a_3+2\cdot3\cdot4a_4x+3\cdot4\cdot5a_5x^2+ \cdots +n(n-1)(n-2)a_nx^{n-3}+\cdots\] \[\cdots\cdots\cdots\cdots\] \[f^{(n)}(x)= n!a_n+(n+1)!a_{n+1}x+\frac{(n+2)!}{2}a_{n+2}x^2+\cdots\] そして\(x=0\)つまり\(f^{(n)}(0)\)について考えると\(x\)を係数に持つ項が消えて \[f^{(n)}(0)= n!a_n\] が残る。これを\(a_n\)についてまとめると \[a_n=\frac{f^{(n)}(0)}{n!}\] よって求める関数\(f(x)\)は以下の様になる \[f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\cdots+\frac{f^{(n)}(0)}{n!}x^n+\cdots=\sum^\infty_{k=0}\frac{f^{(k)}(0)}{k!}x^k\] この級数展開は\(x=0\)周りで展開する方法で一般にマクローリン展開（Maclaurin expansion)として知られており、 その級数はマクローリン級数（Maclaurin　series）と呼ばれる。 これに対して関数の任意の場所\(a\)の周りで展開する為に\(x\)を\((x-a)\)に置き換えたもの、すなわち \[f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n+\cdots=\sum^\infty_{k=0}\frac{f^{(k)}(a)}{k!}(x-a)^k\] で与えられる級数をテイラー級数(Taylor series)、テイラー級数に展開することをテイラー展開(Taylor expansion)という。
• テイラー展開とその応用
• テイラー展開は工学上の応用として微小区間、微小時間など微小量を扱う微分や微分方程式などでしばしば利用される。
  一見非線形に見える現象においても微小量においては線形とみなすことで問題を取り扱いやすくすることが可能になる。
  例えばx軸上の一次元物理量を扱う問題において物理量\(u(x)\)に対して\(u(x+\Delta x)\)はテイラー展開の\((x-a)\Rightarrow\Delta x\)として一次近似することで \[u(x+\Delta x)\simeq u(x)+\frac{du}{dx}\Delta x\] となり線形問題に帰着させることができる
• 関数のテイラー展開（マクローリン展開）
• 三角関数
\[\sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+ \cdots = \sum^\infty_{k=0}\frac{(-1)^k}{(2k+1)!}x^{(2k+1)}\] \[\cos(x)=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+ \cdots = \sum^\infty_{k=0}\frac{(-1)^k}{(2k)!}x^{(2k)}\]
• 指数関数
\[e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+\frac{x^4}{4!}+ \cdots = \sum^\infty_{k=0}\frac{x^k}{k!}\]
• 複素指数関数
\begin{eqnarray} e^{ix}&=&1+ix-\frac{x^2}{2!}-i\frac{x^3}{3!}+\frac{x^4}{4!}+ \cdots \\ &=& (1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}+ \cdots) + i(x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+ \cdots) \\ &=& \sum^\infty_{k=0}\frac{(-1)^k}{(2k)!}x^{(2k)} + i\sum^\infty_{k=0}\frac{(-1)^k}{(2k+1)!}x^{(2k+1)}\\ &=& \cos(x)+i\sin(x)\\ \end{eqnarray} \[(\because i^2=-1)\] ここで\(x=\pi\)のとき \[e^{i\pi}=\cos(\pi)+i\sin(\pi)=-1\] より \[e^{i\pi}+1=0\]

---

プログラムでの実装

---

• サンプルプログラムの概要
三角関数（sin(x),cos(x)）と指数関数(exp(x))をテイラー展開で近似を行う。
近似は第１項から第３０項までの近似を行う。近似の項数は画面左上に表示され、上下キーで 項数を増減させる。 左右キーで左右にシフトさせることができる。 また関数の選択はメニューにて切り替える。

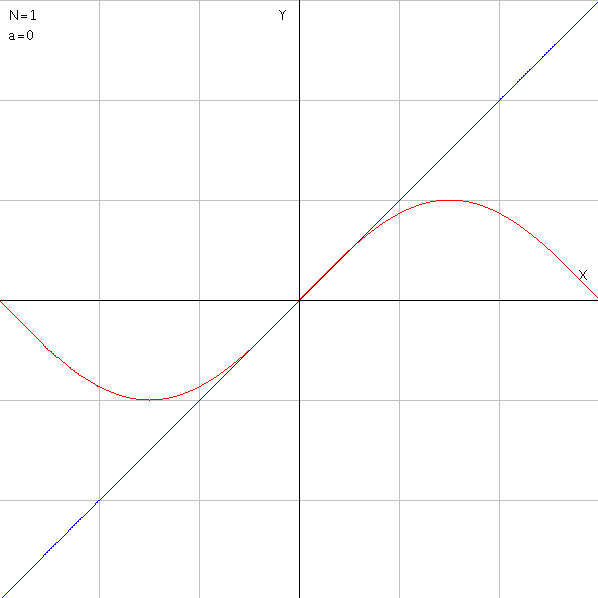
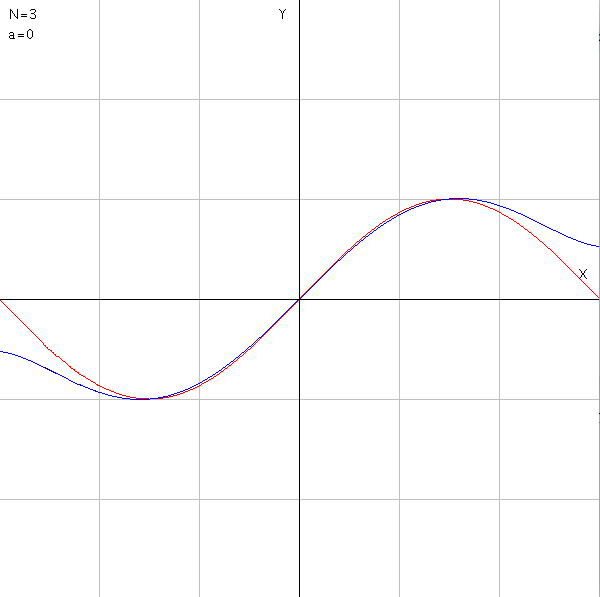
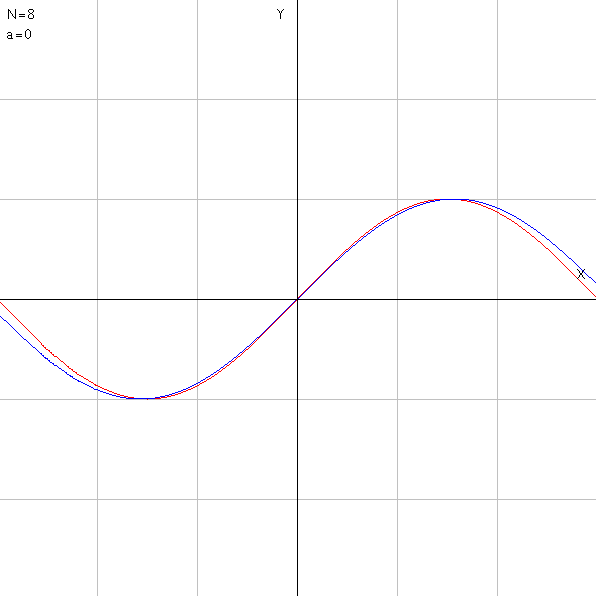
      //sin(x)のテイラー展開
      for(int i=0;i<n;i++) {
        for(int j=0;j<order;j++) {
          y[i]+=Math.pow(-1, j)*Math.pow(x[i]-a, 2*j+1)/fact(2*j+1);
        }
      }

      

第１項までの近似	第３項までの近似	第８項までの近似

GIF画像


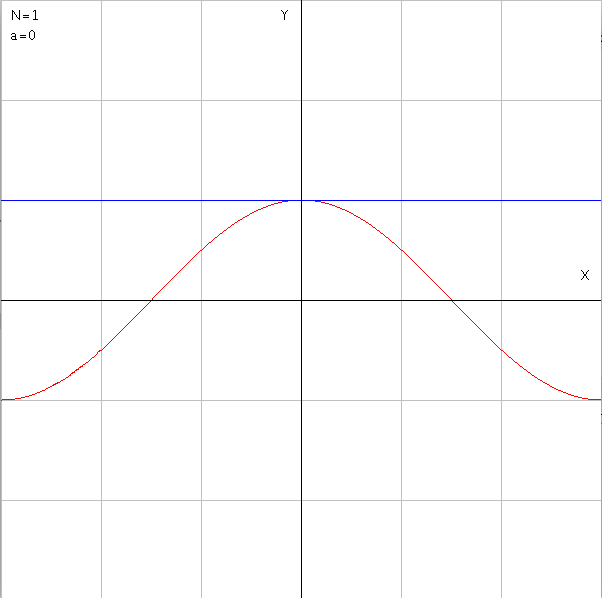
      //cos(x)のテイラー展開
      for(int i=0;i<n;i++) {
				for(int j=0;j<order;j++) {
					y[i]+=Math.pow(-1, j)*Math.pow(x[i]-a, 2*j)/fact(2*j);
				}
      }

      

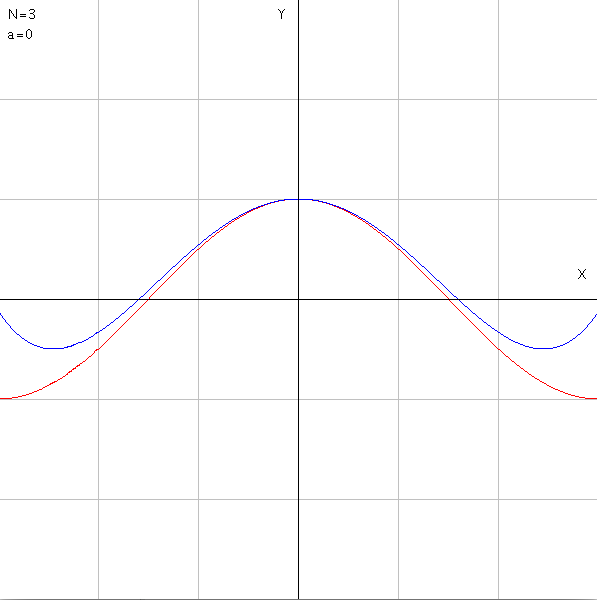
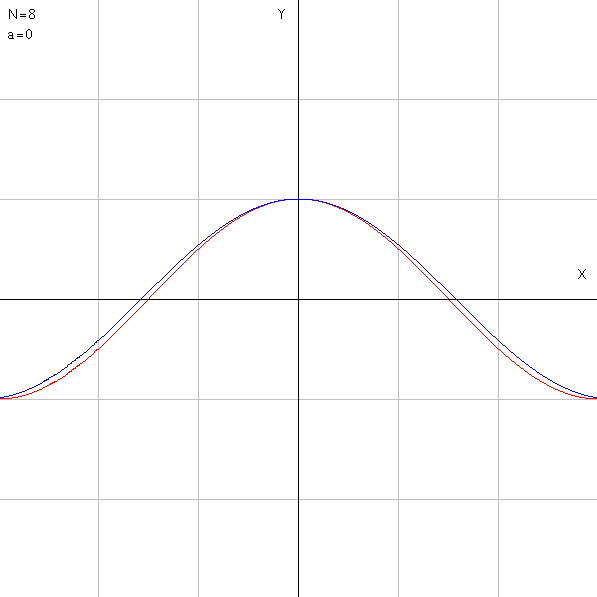
第１項までの近似	第３項までの近似	第８項までの近似

GIF画像


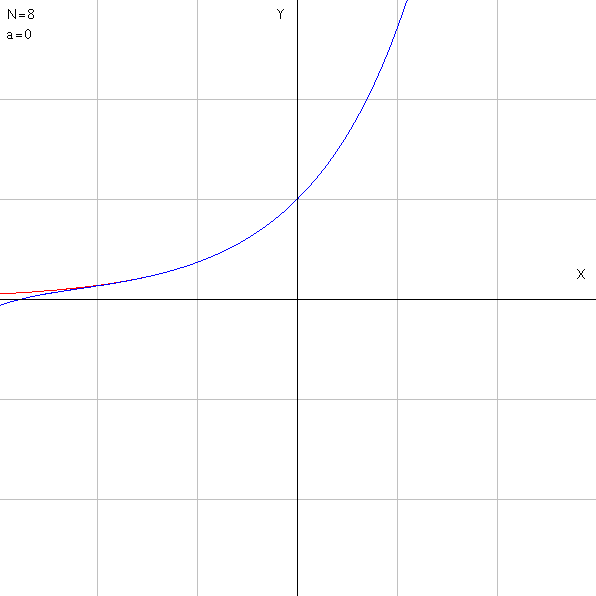
      //exp(x)のテイラー展開
      for(int i=0;i<n;i++) {
				for(int j=0;j<order;j++) {
					y[i]+=Math.pow(x[i]-a, j)/fact(j);
				}
      }

      

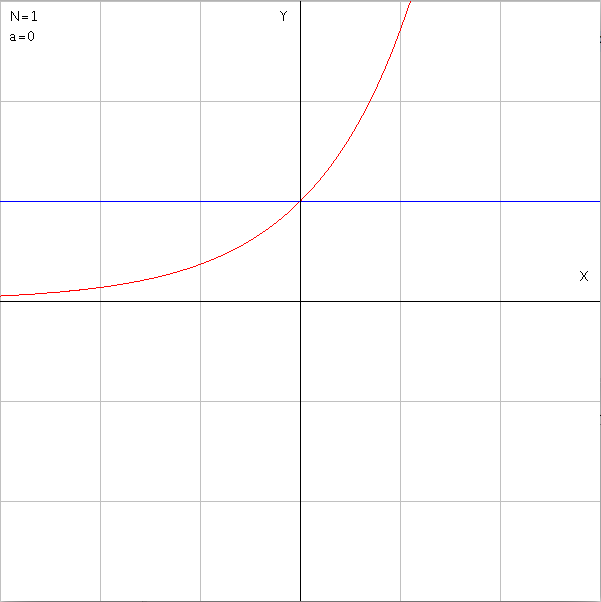
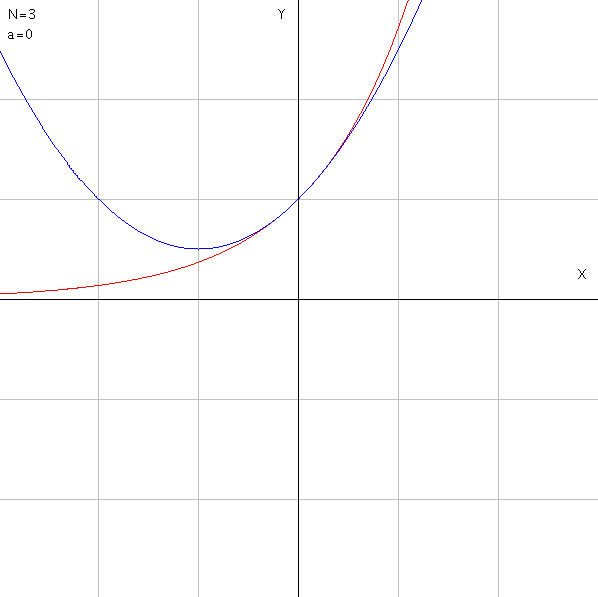
第１項までの近似	第３項までの近似	第８項までの近似

GIF画像
サンプルプログラム（実行可能JARファイル）
サンプルコード