拡散方程式

• 拡散
• 拡散(diffusion)は粒子などが拡がり、散らばってゆくような物理現象で日常の中でもよく観察される。例えば水の中にインクを１滴落とすと水全体に拡がってゆくような様子などが挙げられる。

初期状態	一定時間経過した状態	十分時間経過した状態

• 拡散方程式
• 拡散方程式は拡散の様子モデル化したものである
• 拡散方程式は一般に左辺に粒子密度uに関する時間tの一階微分、右辺に粒子密度uに関する空間の２階微分をもつ偏微分方程式として表される。

  拡散方程式 \[ \frac{\partial u}{\partial t} = D_u \Delta u \] Duは拡散係数を表す。 Δuは粒子密度uのラプラシアンで、空間がxのみの1次元の場合は以下のようになる \[\frac{\partial u}{\partial t} = D_u\frac{\partial^2 u}{\partial x^2}\] x,yの２次元の場合、以下のようになる \[\frac{\partial u}{\partial t} = D_u(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2})\]

• 拡散方程式の導出
• 1次元における拡散の様子を考える。x軸上に粒子uがあるとする。この粒子uは常にx軸上を左右に動いており、微小時間Δt毎に等確率で左右に移動するものとする。 つまり1/2の確率で左に、1/2の確率で右に移動する。粒子uについてx軸上の位置と時刻の関数として \[u(x,t)\] とすると、微小時間Δt経過した時の粒子uの位置は期待値を用いて以下の様に記述される \[u(x,t+\Delta t)=\frac{1}{2}u(x+\Delta x)+\frac{1}{2}u(x-\Delta x)\] 両辺をそれぞれテイラー展開して、Δtを十分小さいものとして左辺を一次近似、右辺を二次近似すると \[u(x,t+\Delta t)=u+\frac{\partial u}{\partial t}\Delta t+\frac{\partial ^2u}{\partial t^2}\frac{\Delta t^2}{2}+ \cdots \simeq u+\frac{\partial u}{\partial t}\Delta t\] \[\frac{1}{2}u(x+\Delta x)+\frac{1}{2}u(x-\Delta x)=\frac{1}{2}(u+\frac{\partial u}{\partial x}\Delta x+\frac{\partial ^2u}{\partial x^2}\frac{\Delta x^2}{2}+ \cdots )+ \frac{1}{2}(u-\frac{\partial u}{\partial x}\Delta x+\frac{\partial ^2u}{\partial x^2}\frac{\Delta x^2}{2}+ \cdots ) \\ \simeq u+\frac{\partial ^2u}{\partial x^2}\frac{\Delta x^2}{2}\] 以上を整理すると拡散方程式が得られる \[\frac{\partial u}{\partial t}=D\frac{\partial^2 u}{\partial x^2}\] \[(D=\frac{\Delta x^2}{2\Delta t})\]
• 2次元の場合は左右上下の4方向に等確率で各方向に1/4の確率で移動することを考えれば1次元の考えをそのまま拡張することができる \[u(x,t+\Delta t)=\frac{1}{4}u(x+\Delta x)+\frac{1}{4}u(x-\Delta x)+\frac{1}{4}u(x+\Delta y)+\frac{1}{4}u(x-\Delta y)\] この式を1次元の場合と同様にテイラー展開して整理すると以下の式が得られる \[\frac{\partial u}{\partial t}=D(\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2})\] \[(D=\frac{\Delta x^2}{4\Delta t})\] この場合2次元の濃度勾配を表すものとして、ナブラ演算子\(\nabla\)を使えば以下のように表される。 \[\frac{\partial u}{\partial t}=D\nabla^2u\] \[(\nabla=\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}, \nabla^2=\frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2})\] またラプラス演算子（ラプラシアン）\(\Delta\)を使って以下のようにも表すことができる \[\frac{\partial u}{\partial t}=D\Delta u\] \[(\nabla^2=\Delta)\]

プログラムでの実装

• サンプルプログラム（粒子運動のシミュレーション）の概要
粒子を実際にランダムに動かすことによってミクロでの拡散の様子を観察する。簡単のため粒子は左右上下の４方向にのみ動くものとし、 常に1/4の確率で停止することなく動作するモデルを考えるものとする。またシミュレーション空間は閉鎖空間を仮定しており、シミュレーション領域の外にでることはない。

      //粒子の座標計算
			int x;
			int y;

      //1/4の確率で上下左右に移動する
			switch(rand.nextInt(4)) {
			case 0:
				x=particle[k][0]+1;
				y=particle[k][1];
				break;
			case 1:
				x=particle[k][0]-1;
				y=particle[k][1];
				break;
			case 2:
				x=particle[k][0];
				y=particle[k][1]+1;
				break;
			case 3:
				x=particle[k][0];
				y=particle[k][1]-1;
				break;
			default:
				x=particle[k][0];
				y=particle[k][1];
				break;
			}

      //粒子の移動をシミュレーション空間に制限する
			particle[k][0]=(x<0?0:(x>=N?N-1:x));//xの範囲を０からNまでに制限
			particle[k][1]=(y<0?0:(y>=N?N-1:y));//xの範囲を０からNまでに制限

      

初期状態	一定時間経過した状態	十分時間経過した状態

サンプルプログラム（実行可能JARファイル）

サンプルコード
• 拡散方程式
粒子運動をマクロに捉えることにより熱などの物理量として扱うことができる。粒子運動は拡散方程式によりモデル化が可能である。 ここでは1次元と2次元の拡散方程式によるモデルを示す
• 1次元拡散方程式のプログラム
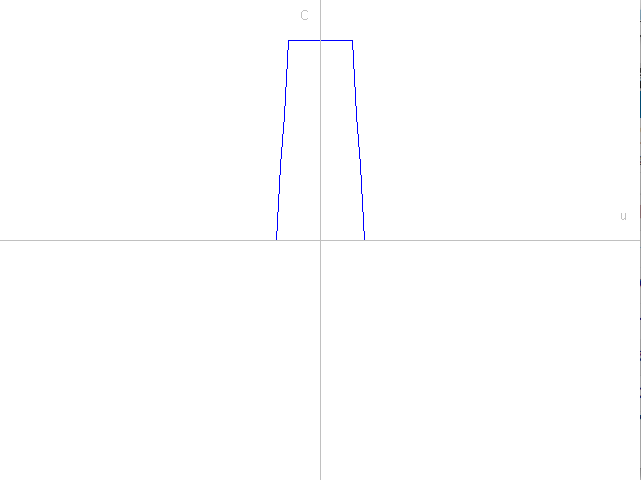
1次元拡散方程式のプログラムでは縦軸を物理量（熱など）、横軸を空間とした時間発展のグラフをアニメーションで表示する
• 数値微分(差分法)
拡散方程式には微分項が含まれているため何らかの方法で微分を記述する必要がある。 コンピュータでは微分のような連続の式は扱えないので、差分によって近似する。（差分法）
1階の微分は以下のように近似する（hは十分小さいとする) \[\frac{du}{dt} = \lim_{dt \to 0} \frac{u(t+dt)-u(t)}{dt}\] \[\approx \frac{u(t+h)-u(t)}{h}\] 2階の微分は以下のように近似する \[\frac{d^2u}{dt^2} = \lim_{dt \to 0} \frac{\frac{d}{dt}u(t+dt)-\frac{d}{dt}u(t)}{dt}\] \[\approx \frac{1}{h}\frac{u(t+2h)-u(t+h)-u(t+h)+u(t)}{h}\] \[=\frac{u(t+2h)-2u(t+h)+u(t)}{h^2}\] ここで差分の中心を-hシフトさせて、最終的に以下のように近似できる \[\frac{d^2u}{dt^2} \approx \frac{u(t+h)-2u(t)+u(t-h)}{h^2}\]

        //差分法（拡散方程式　右辺）
        for(int i=1;i<n-1;i++) {
          yn[i]=dt*Du*(y[i-1]-2.0*y[i]+y[i+1])/(h*h);
        }
    
        //値の更新（拡散方程式　左辺）
        for(int i=1;i<n-1;i++) {
          y[i]=y[i]+yn[i];
        }
    
        /*
        //境界条件（ディレクリ条件）
        y[0]=0.0;
        y[n-1]=0.0;
        */
    
        //境界条件（ノイマン条件）
        y[0]=y[1];
        y[n-1]=y[n-2];
    

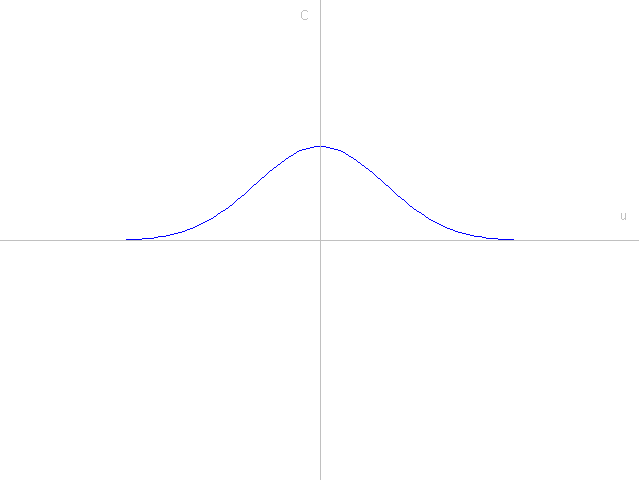
初期状態	一定時間経過した状態	十分時間経過した状態

サンプルプログラム（実行可能JARファイル）

サンプルコード
• 2次元拡散方程式のプログラム
2次元拡散方程式のプログラムでは画素値（輝度）を物理量、x-y平面をシミュレーション領域とした時間発展のグラフをアニメーションで表示する
• ラプラシアン(2次元)
２つの独立変数x、yをもつ２次元のラプラシアンをx方向の微小区間をi、y方向の微小区間をj、それぞれの増分をhとして以下のように近似する。(i,j,hは十分小さいとする) \[\Delta u = \frac{\partial^2u}{\partial x^2}＋\frac{\partial^2u}{\partial y^2}\] \[ \approx　\frac{u(x+i,y)-2u(x,y)+u(x-i,y)}{h^2}+\frac{u(x,y+j)-2u(x,y)+u(x,y-j)}{h^2}\] \[\frac{u(x+i,y)+u(x-i,y)+u(x,y+j)+u(x,y-j)-4u(x,y)}{h^2}\]
• 拡散方程式の数値計算
\[ \frac{\partial u}{\partial t} = D_u \Delta u \] 与えられた偏微分方程式を差分で近似すると以下のようになる（hは十分小さいとする） \[ \begin{eqnarray} \left\{ \begin{array}{l} \frac{u(x,y,t+dt)-u(x,y,t)}{dt} = D_u \Delta u \end{array} \right. \end{eqnarray} \] 両辺にdtをかけて、整理すると最終的に以下のようになる \[ \begin{eqnarray} \left\{ \begin{array}{l} u(x,y,t+dt) = u(x,y,t)+D_u \Delta u \end{array} \right. \end{eqnarray} \] 以上の内容をJavaのコードで記述すると以下のようになる

    //ラプラシアンの数値計算
    //laplacian_uはUについてのラプラシアン、hは微小増分に対応
    laplacian_u=(u[i+1][j]+u[i][j+1]+u[i-1][j]+u[i][j-1]-4*u[i][j])/(h*h);
    
    //拡散方程式の数値計算
    //Duはの拡散係数
    dudt=Du*laplacian_u;
    
    //差分の更新
    u1[i][j]=u[i][j]+dt*dudt;
    

• サンプルプログラム概要
拡散方程式によるシミュレーションを行い、時間によって変化する物質の濃度パターンをアニメーションで表示する。

初期状態	一定時間経過した状態	十分時間経過した状態

サンプルプログラム（実行可能JARファイル）

サンプルコード
• サンプルプログラム概要
拡散方程式によるシミュレーションを行い、時間によって変化する物質の濃度パターンをアニメーションで表示する。

初期状態	一定時間経過した状態	十分時間経過した状態

サンプルプログラム（実行可能JARファイル）

サンプルコード

• 参考文献
• 岩山　隆寛, 地球惑星科学基礎III 第6章 拡散方程式, https://www.se.fukuoka-u.ac.jp/iwayama/teach/kisoIII/2015/chap6.pdf