反応拡散モデル

• チューリングパターン
• 1952年のアラン・チューリング(Alan Mathieson Turing)の論文「The Chemical Basis of Morphogenesis」で発表された数理モデル（反応拡散モデル）で生成されるパターン
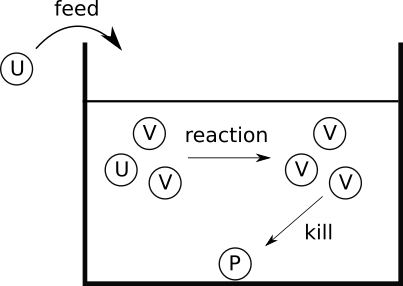
• 動物の表皮のパターンなど、自然界に存在する様々なパターンの生成過程を拡散（diffusion）と化学反応(reaction)の組み合わせでモデル化

Pomacanthus imperator BY Jordi Payà (CC BY-ND 2.0) https://www.flickr.com/photos/arg0s/14162350619

• 反応拡散方程式
• 拡散方程式に反応の式を組み合わせたもの
• 拡散を表す拡散項と反応を表す反応項の和を右辺にもつ偏微分方程式として表される。

  ２成分（２種類の物質U,Vの濃度u,v）の拡散反応方程式 \[ \frac{\partial u}{\partial t} = D_u \Delta u + F(u,v) \] \[ \frac{\partial v}{\partial t} = D_v \Delta v + G(u,v) \] 第１項は拡散項でDu,Dvは拡散係数を表す。Δu,Δvはそれぞれu,vのラプラシアンでx,yの２次元の場合、以下のようになる \[\Delta u = \frac{\partial^2 u}{\partial x^2}+\frac{\partial^2 u}{\partial y^2}\] \[\Delta v = \frac{\partial^2 v}{\partial x^2}+\frac{\partial^2 v}{\partial y^2}\] 第２項は反応項でF(u,v)、G(u,v)は局所的な反応を示すu,vについての関数で表される。

• Gray-Scottモデル
　F(u,v)、G(u,v)がそれぞれ以下のものはGray-Scottモデルとして知られている。(PearsonのGray-Scottモデル) \[F(u,v) = -uv^2 + f(1-u)\] \[G(u,v) = uv^2 - v(f+k)\] ここで、fはuの補充率(feed rate)、kはvの減衰率(kill rate)を表す。
全体としては以下のようになる。 \[ \frac{\partial u}{\partial t} = D_u \Delta u - uv^2 + f( 1 - u ) \] \[ \frac{\partial v}{\partial t} = D_v \Delta v + uv^2 - v( f + k ) \]

• Gray-Scottモデルにおける化学反応モデル
• Gray-Scottモデルは1983年にGray(Peter H.K. Gray)とScott(Steven K. Scott)が発表 (AUTOCATALYTIC REACTIONS IN THE ISOTHERMAL, CONTINUOUS STIRRED TANK REACTOR)
• Gray-Scottモデルでは物質U、Vについての自己触媒反応として以下の化学反応式で与えられる。
\[U + 2V \to 3V \] \[V \to P \]
• １つのUと２つのVが反応して３つのVを生成する
• Vは一定の割合でそれ以上変化しない物質である不活性物質Pに変化する



• 反応速度式
化学反応において反応速度は物質の濃度の積に比例する。 物質U,Vの反応式が以下で与えられた場合、 \[U + 2V \to 3V \] 物質UとVの反応速度をrとすると反応速度は以下のとおりである \[r = uv^2\] 化学反応によってUの密度は微小時間あたりuv²減少し、Vの密度はuv²増加する したがって、それぞれの反応速度r_U,r_Vは以下のようになる \[ r_U=\frac{du}{dt}=-uv^2 \] \[ r_V=\frac{dv}{dt}=uv^2 \]
• 物質の補充と不活性化
Gray-Scottモデルにおいて、物質Uは一定の割合で補充され（流入）、物質Vは一定の割合で不活性化する（流出） 物質Uの補充は補充率fをつかって次のように記述される。物質Uが減少すると減少分（1-u）に比例してUが最大速度fで補充され、物質Uが最大濃度（u=1）に達すると補充が停止する \[ f( 1 - u ) \] 物質Vの不活性化は減衰率kをつかって次のように記述される。 物質Vの濃度に比例して不活性化し、物質Vの濃度が０になると不活性化が停止する \[ v( f + k ) \]
• Gray-Scottモデルの反応速度式
以上をまとめると拡散項を含まないGray-Scottモデルの反応速度式は次のようになる \[ \frac{du}{dt} = - uv^2 + f( 1 - u ) \] \[ \frac{dv}{dt} = uv^2 - v( f + k ) \] この式はu,vの初期濃度やf,kの値によって全く異なる挙動をとり、少しの条件の変化にも敏感に反応する。 これらがある条件を満たせばuとvの濃度が周期的に変化（振動）する振動反応(時計反応)が見られる。 (大抵の場合は平衡状態になる。グラフはパラメータf=0.004,k=0.02。初期条件u=0,v=1でシミュレートしたもの)
自己触媒反応による振動反応として知られている例としてはBZ反応(Belousov-Zhabotinsky reaction)などがある。 >

• 反応拡散系（Gray-Scottモデル）の挙動
拡散項と上記で説明した反応項の組み合わせで、進行波（フラックス）が発生し、パターンを形成する。
1次元の反応拡散系

サンプルコード
2次元の反応拡散系(V成分のみ表示)


実行可能JARファイル
サンプルコード
3次元の反応拡散系(V成分のみ表示)


実行可能JARファイル
JARファイル（ソースコード）

• Gray-Scottモデルにより得られるパターン
• 拡散反応モデルでは初期条件やパラメータ（拡散係数、充填率、減衰率）により様々なパターンが得られる
• 以下に様々な充填率、減衰率の組み合わせにより得られるパターンを示す
• f=0.022,k=0.051

• f=0.04,k=0.06

• f=0.035,k=0.065

• f=0.012,k=0.05

• f=0.025,k=0.05

• f=0.078,k=0.61

• f=0.03,k=0.062

• f=0.039,k=0.058

プログラムでの実装

• 数値微分(差分法)
コンピュータでは微分のような連続の式は扱えないので、差分によって近似する。（差分法）
1階の微分は以下のように近似する（hは十分小さいとする) \[\frac{du}{dt} = \lim_{dt \to 0} \frac{u(t+dt)-u(t)}{dt}\] \[\approx \frac{u(t+h)-u(t)}{h}\] 2階の微分は以下のように近似する \[\frac{d^2u}{dt^2} = \lim_{dt \to 0} \frac{\frac{d}{dt}u(t+dt)-\frac{d}{dt}u(t)}{dt}\] \[\approx \frac{1}{h}\frac{u(t+2h)-u(t+h)-u(t+h)+u(t)}{h}\] \[=\frac{u(t+2h)-2u(t+h)+u(t)}{h^2}\] ここで差分の中心を-hシフトさせて、最終的に以下のように近似できる \[\frac{d^2u}{dt^2} \approx \frac{u(t+h)-2u(t)+u(t-h)}{h^2}\]
• ラプラシアン(2次元)
２つの独立変数x、yをもつ２次元のラプラシアンをx方向の微小区間をi、y方向の微小区間をj、それぞれの増分をhとして以下のように近似する。(i,j,hは十分小さいとする) \[\Delta u = \frac{\partial^2u}{\partial x^2}＋\frac{\partial^2u}{\partial y^2}\] \[ \approx　\frac{u(x+i,y)-2u(x,y)+u(x-i,y)}{h^2}+\frac{u(x,y+j)-2u(x,y)+u(x,y-j)}{h^2}\] \[\frac{u(x+i,y)+u(x-i,y)+u(x,y+j)+u(x,y-j)-4u(x,y)}{h^2}\]
• 反応拡散方程式の数値計算
Gray-scottモデルの反応拡散方程式の近似をおこなう \[ \begin{eqnarray} \left\{ \begin{array}{l} \frac{\partial u}{\partial t} = D_u \Delta u - uv^2 + f( 1 - u ) \\ \frac{\partial v}{\partial t} = D_v \Delta v + uv^2 - v( f + k ) \end{array} \right. \end{eqnarray} \] 与えられた偏微分方程式を差分で近似すると以下のようになる（hは十分小さいとする） \[ \begin{eqnarray} \left\{ \begin{array}{l} \frac{u(x,y,t+dt)-u(x,y,t)}{dt} = D_u \Delta u - uv^2 + f( 1 - u ) \\ \frac{v(x,y,t+dt)-v(x,y,t)}{dt} = D_v \Delta v + uv^2 - v( f + k ) \end{array} \right. \end{eqnarray} \] 両辺にdtをかけて、整理すると最終的に以下のようになる \[ \begin{eqnarray} \left\{ \begin{array}{l} u(x,y,t+dt) = u(x,y,t)+(D_u \Delta u - uv^2 + f( 1 - u ))dt \\ v(x,y,t+dt) = v(x,y,t)+(D_v \Delta v + uv^2 - v( f + k ))dt \end{array} \right. \end{eqnarray} \] 以上の内容をJavaのコードで記述すると以下のようになる

    //ラプラシアンの数値計算
    //laplacian_u,laplacian_vはそれぞれU,Vについてのラプラシアン、hは微小増分に対応
    laplacian_u=(u[i+1][j]+u[i][j+1]+u[i-1][j]+u[i][j-1]-4*u[i][j])/(h*h);
    laplacian_v=(v[i+1][j]+v[i][j+1]+v[i-1][j]+v[i][j-1]-4*v[i][j])/(h*h);
    
    //拡散反応方程式（Gray-Scottモデル）の数値計算
    //Du,Dvはそれぞれu,vの拡散係数、fはuの補充率(feed rate)、kはvの減衰率(kill rate)
    dudt=Du*laplacian_u-u[i][j]*v[i][j]*v[i][j]+f*(1.0-u[i][j]);
    dvdt=Dv*laplacian_v+u[i][j]*v[i][j]*v[i][j]-(f+k)*v[i][j];
    
    //差分の更新
    u1[i][j]=u[i][j]+dt*dudt;
    v1[i][j]=v[i][j]+dt*dvdt;
    

• サンプルプログラム概要
サンプルプログラムは反応拡散モデル（Gray-Scottモデル）によるシミュレーションを行い、 時間によって変化する物質の濃度パターンをアニメーションで表示する。 サンプルプログラム（実行可能JARファイル）
サンプルプログラムの様子


サンプルコード
• シミュレーション条件
• シミュレーション領域
• 領域サイズ：256×256(境界処理用の仮想領域を含めると258×258)
• 要素サイズ：１ピクセル/要素
• 初期条件
• u全体を1.0、v全体を0.0で初期化
• U,Vの領域中央の20×20矩形領域にランダムノイズを付加（0.5≤u<0.6, 0.25≤v<0.35）
• 境界条件
• 周期境界条件
• シミュレーションパラメータ
• dt=1.0
• h=0.01
• Du=2.0×10^-5
• Dv=1.0×10^-5
• f=0.04
• k=0.06
• 表示
• 物質Vの濃度パターンを２５６段階のグレースケール表示
• シミュレーション領域２５６×２５６ピクセル表示
• 参考文献
• 三井 和男, デザイン言語　Processing入門 - 楽しく学ぶコンピュテーショナルデザイン
• 岡 瑞起, 池上 高志, ドミニク・チェン, その他, 作って動かすALife ―実装を通した人工生命モデル理論入門
• Karl Sims, Reaction-Diffusion Tutorial, http://karlsims.com/rd.html
• 尾崎　淳, 反応拡散系（Reaction-Diffusion system）, http://www.fbs.osaka-u.ac.jp/labs/skondo/ozaki/what%20is%20RD%202(outline).htm
• A. M. Turing, The Chemical Basis of Morphogenesis, Philosophical Transactions of the Royal Society, 1952.
• P. Gray and S.K. Scott, “Autocatalytic reactions in the isothermal, continuous stirred tank reactor. Isolas and other forms of multistability,” 1983
• 土屋荘次, 平川暁子 物質の科学・反応と物性, https://info.ouj.ac.jp/~hamada/TextLib/rm/chap12/Text/Cr991205.html