- 単振り子(Simple pendulum) 片方が天井に接続された長さ\(l\)の伸びやたわみのない質量が無視できる糸(もしくは棒)のもう片方に質量\(m\)の直径が無視できるほど小さい小球をつけた単振り子の運動について考える。
初期状態として鉛直方向から角度\(\phi_0\)になる様に持ち上げて静かに離した状態を想定する。(つまり初速度が0)
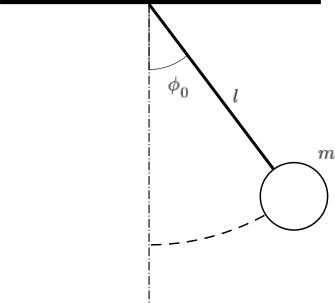
単振り子
小球には下向きに重力がかかるが糸に接続されており動径方向(糸と天井との接続点と小球の中心を結ぶ直線方向)は固定されている(力がつりあっている)為、力の分解により
方位角方向(糸と天井との接続点を中心とした半径\(l\)の円弧の接線方向)に向かう。
そのため小球は常に方位角方向に向かう円運動をする。
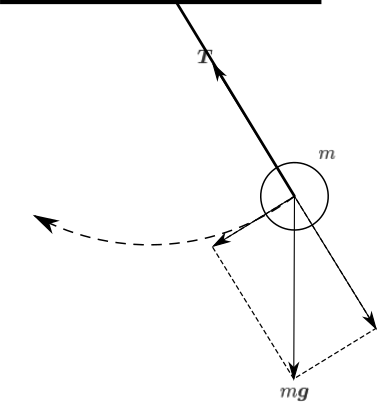
力の分解と円運動
円運動や回転運動を記述する場合、様々な方法があるが動径方向と方位角方向で位置を記述する極座標系で考えると便利である。しかしコンピュータシミュレーションで運動を視覚化する場合、コンピュータの座標系に合わせる必要がある。
コンピュータの座標系は一般にxを横軸、yを縦軸とする直交座標系であるため、最終的には直交座標系に変換する必要がある。
そこで今回は単振り子の運動をまず極座標系で記述して、直交座標系に変換することにする。
- 直交座標系と極座標系 糸と天井の接続点を原点\(O\)として、小球の位置を位置ベクトル\(\mathbf{r}\)とすると、
直交座標系では以下の様に記述できる。 \[\mathbf{r}(x,y)=x\mathbf{e}_x+y\mathbf{e}_y\] ここで\(\mathbf{e}_x\)、\(\mathbf{e}_y\)は直交座標系の基底ベクトル(この場合、x軸方向とy軸方向の単位ベクトル)でそれぞれ以下の通りである。 \[\mathbf{e}_x=\left(\begin{array}{c}1\\0\end{array}\right),\mathbf{e}_y=\left(\begin{array}{c}0\\1\end{array}\right)\] つまり位置ベクトル\(\mathbf{r}\)は基底ベクトルの定数倍の和(線形結合)で表現できることを意味する。
一方、極座標系では以下の様に記述できる。 \[\mathbf{r}(r,\phi)=r\mathbf{e}_r\] 基底ベクトル(この場合、動径方向と方位角方向の単位ベクトル)は \[\mathbf{e}_r=\left(\begin{array}{c}1\\0\end{array}\right),\mathbf{e}_\phi=\left(\begin{array}{c}0\\1\end{array}\right)\] となる。
つまり極座標系における位置ベクトル\(\mathbf{r}\)は動径方向の単位ベクトルの定数倍のみで表現できることを意味する。
直交座標系を基準に考えると動径方向や方位角方向は位置ベクトル(この場合、物体の位置)によって変化するため、基底ベクトルも位置ベクトルによって変化している様に見えることに注意。

直交座標系と極座標系における表現
ここで直交座標系と極座標系との関係を示す為に極座標系の基底ベクトルを直交座標系の基底ベクトルで表す。
\[\mathbf{e}_r=\sin\phi(t)\mathbf{e}_x+\cos\phi(t)\mathbf{e}_y\]
\[\mathbf{e}_\phi=\cos\phi(t)\mathbf{e}_x-\sin\phi(t)\mathbf{e}_y\]
\(\phi(t)\)は角度の時間変化を表す関数で時間の関数になっている。この式からも物体が運動した場合、直交座標系を基準に考えると極座標系の基底ベクトルが変化していることがわかる。
さらにこれらの2式を時間微分すると表記の簡略化のためNewton式の微分記号(\(\frac{dy}{dt}=\dot{y}\))を用いて \[\mathbf{\dot{e}}_r=\dot{\phi}(t)\{\cos\phi(t)\mathbf{e}_x-\sin\phi(t)\mathbf{e}_y\}=\dot{\phi}(t)\mathbf{e}_\phi \] \[\mathbf{\dot{e}}_\phi=-\dot{\phi}(t)\{\sin\phi(t)\mathbf{e}_x-\cos\phi(t)\mathbf{e}_y\}=-\dot{\phi}(t)\mathbf{e}_r \] ここで\(\phi(t)\)は時間の関数なので合成関数の微分になっていることに注意。
以上から直交座標系と極座標系の関係を調べることで、極座標系の基底ベクトルの微分はそれぞれ反時計回りに90°回転させる性質があることがわかる。
- 極座標系における運動方程式の導出 今回の目的は円運動する物体の運動を調べることなので、極座標系での速度と加速度に相当する位置ベクトルの時間に関する1階微分と2階微分を求める。 極座標形式の位置ベクトル \[\mathbf{r}(r,\phi)=r\mathbf{e}_r\] の1階微分は \[\dot{\mathbf{r}}(r,\phi)=\dot{r}\mathbf{e}_r+r\dot{\mathbf{e}}_r=\dot{r}\mathbf{e}_r+r\dot{\phi}(t)\mathbf{e}_\phi\] \[(\because\mathbf{\dot{e}}_r=\dot{\phi}(t)\mathbf{e}_\phi)\] 2階微分は \[ \begin{eqnarray} \ddot{\mathbf{r}}(r,\phi)&=&\ddot{r}\mathbf{e}_r+\dot{r}\dot{\mathbf{e}}_r+\dot{r}\dot{\phi}(t)\mathbf{e}_\phi+r\ddot{\phi}(t)\mathbf{e}_\phi+r\dot{\phi}(t)\dot{\mathbf{e}}_\phi\\ &=&(\ddot{r}-r\dot{\phi}(t)^2)\mathbf{e}_r+(2\dot{r}\dot{\phi}(t)+r\ddot{\phi}(t))\mathbf{e}_\phi \end{eqnarray} \] \[(\because\mathbf{\dot{e}}_r=\dot{\phi}(t)\mathbf{e}_\phi, \mathbf{\dot{e}}_\phi=-\dot{\phi}(t)\mathbf{e}_r)\] ここで振り子の小球にかかる力についての運動方程式をたてると \[\mathbf{F}=m\mathbf{a}\]より動径方向の運動方程式は \[\mathbf{F}_r=m(\ddot{r}-r\dot{\phi}(t)^2)=mg\cos\phi(t)-\mathbf{T}\] 方位角方向の運動方程式は \[\mathbf{F}_\phi=m(2\dot{r}\dot{\phi}(t)+r\ddot{\phi}(t))=-mg\sin\phi(t)\]
- 動径方向の運動方程式 小球は長さ\(l\)の糸に接続しているため原点\(O\)からの距離\(r\)について \[r=l\] となり、伸びやたわみがなく時間変化しないため、動径方向の時間微分\(\dot{r}=0\)より \[\ddot{r}=0\] なので \[-ml\dot{\phi}(t)^2=mg\cos\phi(t)-\mathbf{T}\] になる。 ここで重力の動径方向成分\(mg\cos\phi(t)\)と糸の張力\(\mathbf{T}\)は常に釣り合っているため、 \[-ml\dot{\phi}(t)^2=0\] \[\dot{\phi}(t)=0\] となり動径方向の速度は発生しない
- 方位角方向の運動方程式 \(r=l\),\(\dot{r}=0\)より \[ml\ddot{\phi}(t)=-mg\sin\phi(t)\] \[\ddot{\phi}(t)=-\omega^2\sin\phi(t) \ \ \ (\omega=\sqrt{\frac{g}{l}})\] 微小時間(\(t\ll1\))の変化と仮定すると、\(\phi(t)\ll1\)となり、テイラー展開の1次近似により \[\ddot{\phi}(t)=-\omega^2\phi(t) \ \ \ (\because \sin\phi(t)\simeq\phi(t))\] と2階の線形微分方程式として解くことができる。 ここで \[\phi(t)=e^{\lambda t}\] と置くと運動方程式は次のようになる \[\lambda^2e^{\lambda t}=-\omega^2e^{\lambda t}\] \[\lambda^2=-\omega^2\] \[\lambda=\pm i\omega \ \ \ (i^2=-1)\] よって与えられた微分方程式の解の候補として \[\phi(t)_1=e^{+i\omega t}, \phi(t)_2=e^{-i\omega t}\] が得られる。 複数の解の定数倍の線形結合もまた解となることから一般解は次のように書ける。 \[\phi(t)=C_1 e^{+i\omega t} + C_2e^{-i\omega t}\ \ \ (C_1, C_2は任意定数)\] オイラーの公式\(e^{\pm i\omega t}=\cos\omega t \pm i \sin\omega t\)を使って \[\phi(t)=(C_1 + C_2)\cos\omega t+(C_1-C_2) i \sin\omega t\] 任意定数を\(C_1=\frac{A_1-A_2 i}{2}, C_2=\frac{A_1+A_2 i}{2}\)とすると一般解 \[\phi(t)=A_1\cos\omega t+A_2 \sin\omega t\] が得られる。 小球を鉛直方向から角度\(\phi_0\)になるように持ち上げて静かに離した状態を想定するので、 初期条件を\(\phi(0)=\phi_0\), \(\dot{\phi}(0)=0\)と設定して特殊解を求めればよい \[\phi(0)=A_1\cos0+A_2\sin0=\phi_0\] \[A_1=\phi_0\] \[\dot{\phi}(0)=-A_1\omega\sin0+A_2\omega\cos0=0\] \[A_2=0\] より単振り子の角度に関する特殊解 \[\phi(t)=\phi_0\cos\omega t\] が得られた。
- 極座標系から直交座標系に変換 これまでは回転運動を記述する為に極座標系において運動方程式を立てて、動径方向の運動、及び方位角方向の動きについての情報を得ることができた。
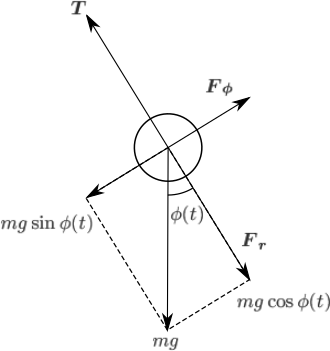
小球にかかる力
最初の初期条件とは異なり初速度を\(v_0\)とする場合は
初期条件を\(\phi(0)=\phi_0\), \(\dot{\phi}(0)=v_0\)と設定して特殊解を求めればよい \[\phi(0)=A_1\cos0+A_2\sin0=\phi_0\] \[A_1=\phi_0\] \[\dot{\phi}(0)=-A_1\omega\sin0+A_2\omega\cos0=v_0\] \[A_2=\frac{v_0}{\omega}\] より単振り子の角度に関する特殊解 \[\phi(t)=\phi_0\cos\omega t+\frac{v_0}{\omega}\sin\omega t\] が得られる。
最後にコンピュータ上にシミュレーション結果を表示する為に直交座標系に変換を行う。
単振り子の運動は動径方向の動きはなく、方位角方向の動きのみなので原点\(O\)から小球までの距離\(l\)と時刻\(t\)における鉛直方向(y軸)との角度\(\phi(t)\)がわかれば 直交座標系の座標を簡単に得ることができる。
変換の関係式は以下の通りである。 \[x=l\sin\phi(t)\] \[y=l\cos\phi(t)\]
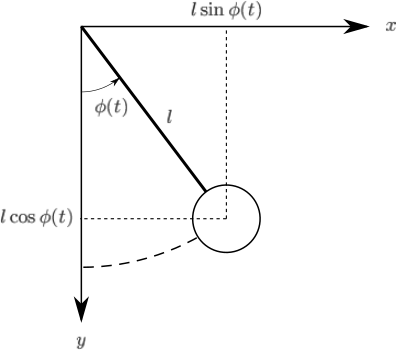
極座標系から直交座標系への変換
プログラムでの実装
- サンプルプログラムの概要 単振り子の物理シミュレーションを行うプログラムで、何らかのキー入力を実行すると単振り子運動が開始する。 シミュレーション条件は固定で
- 重力加速度 \(g=9.8[m/s^2\)
- 回転半径 \(l=400[m]\)
- 振り角 \(\phi_0)=30[°]\)
- 初速度 \(v_0=0[m/s]\)
 サンプルプログラム(実行可能JARファイル)
サンプルプログラム(実行可能JARファイル)